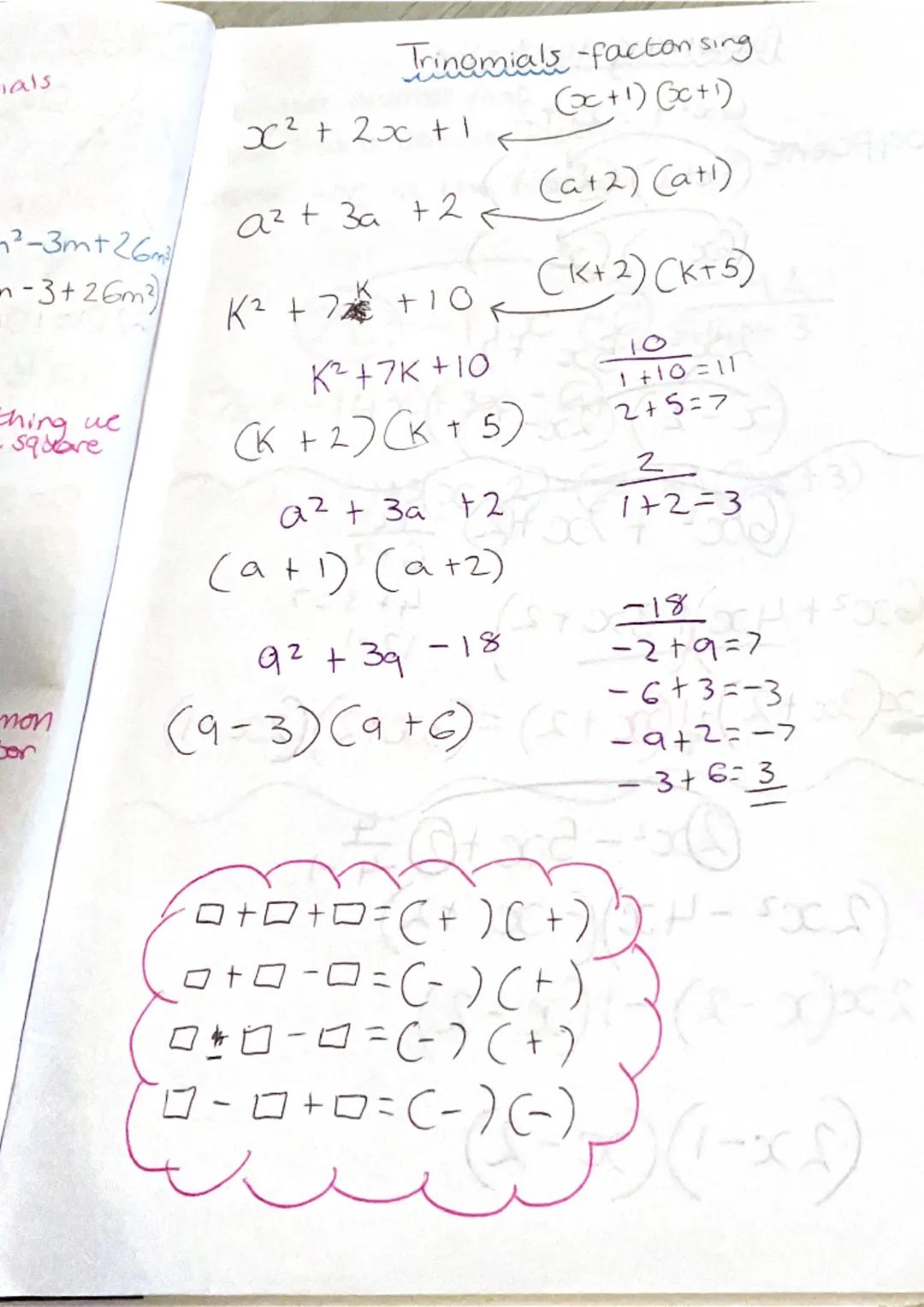This transcript covers various mathematical topics including multiplying and simplifying expressions, solving equations, factoring, and trigonometry. Here's a summary incorporating the guidelines:
A comprehensive guide to essential math concepts for students, covering multiplying and simplifying BODMAS steps, solving trigonometry with right-angled triangles, and factorising trinomials with examples. Key topics include:
- Expanding and simplifying algebraic expressions
- Multiplying brackets and factoring
- Solving equations using BODMAS
- Pythagoras theorem and trigonometry basics
- Factorising trinomials and quadratic expressions