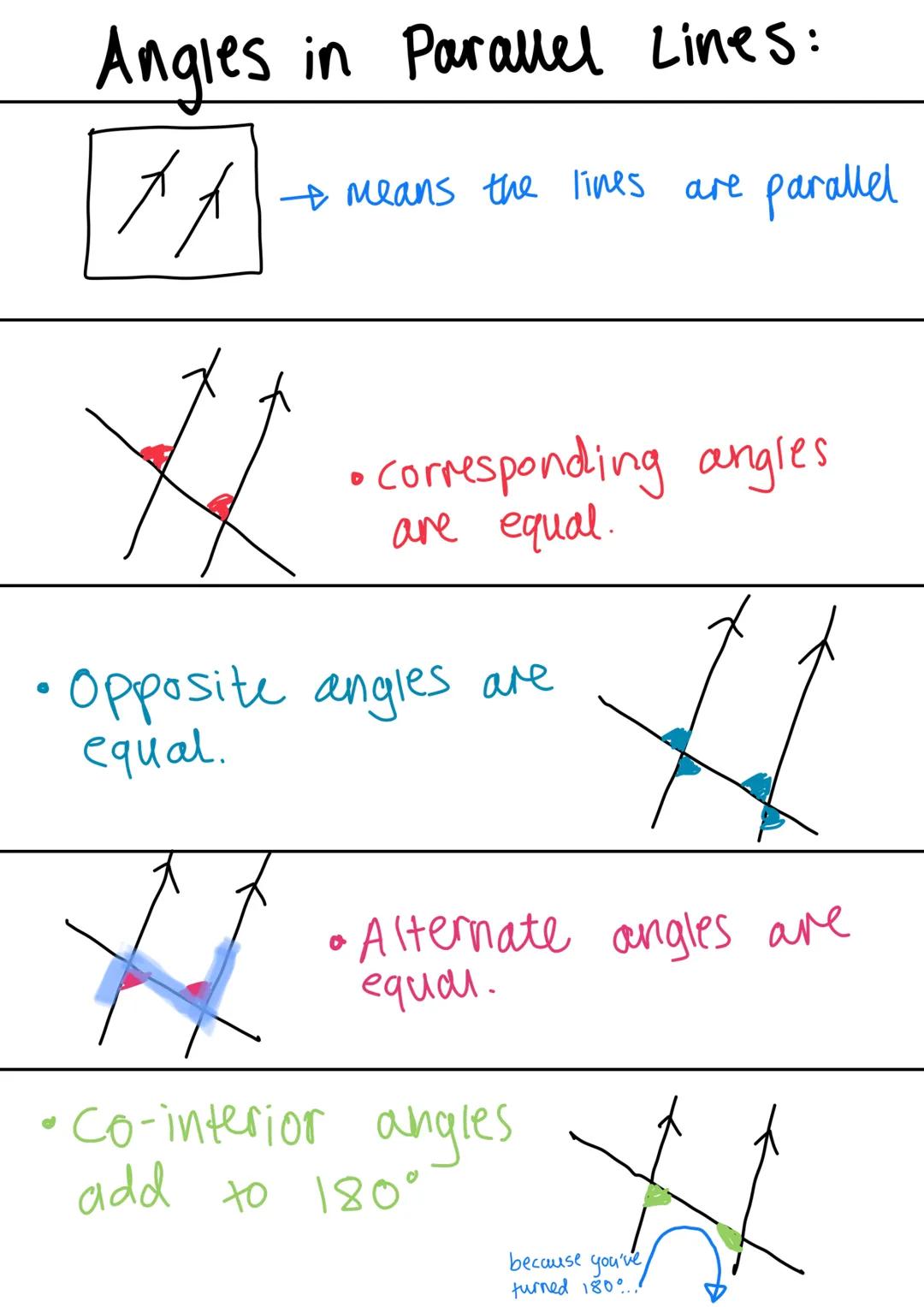
Angles in parallel lines are a fundamental concept in geometry, crucial for GCSE maths angles in parallel lines rules. This guide explores the key principles and relationships between angles formed when parallel lines are intersected by a transversal.
- Parallel lines never intersect and maintain a constant distance between them.
- When a transversal crosses parallel lines, it creates several types of angles with specific properties.
- Understanding these angle relationships is essential for solving angles in parallel lines questions and answers.