A Level simultaneous equationspractice guide covering various question types... Show more
Sign up to see the contentIt's free!
Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy






![SIMULTANEOUS EQUATIONS
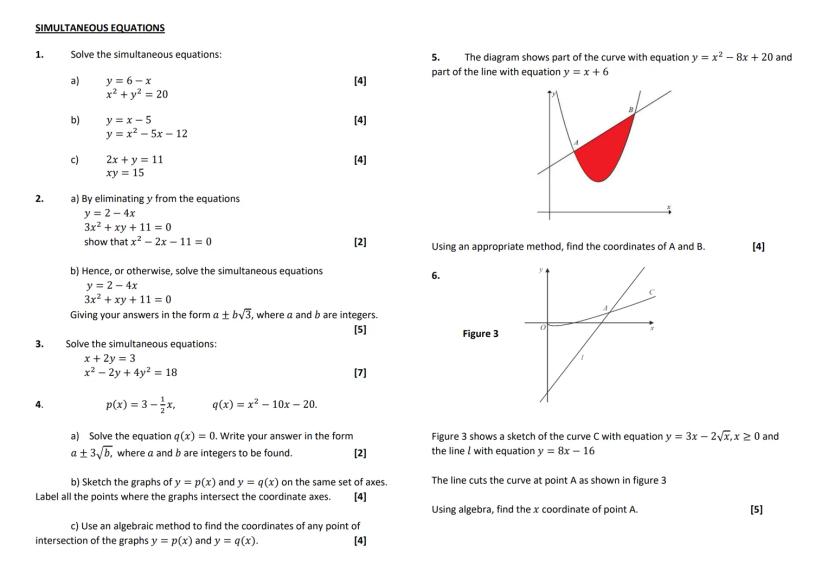
1. Solve the simultaneous equations:
a) $y = 6 - x$
$x^2 + y^2 = 20$ [4]
b) $y = x - 5$
$y = x^2 - 5x - 12$](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FhispBneKVjQVSLLYjXJf_image_page_1.webp&w=2048&q=75)
![SIMULTANEOUS EQUATIONS
1. Solve the simultaneous equations:
a) $y = 6 - x$
$x^2 + y^2 = 20$ [4]
b) $y = x - 5$
$y = x^2 - 5x - 12$](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FhispBneKVjQVSLLYjXJf_image_page_2.webp&w=2048&q=75)
![SIMULTANEOUS EQUATIONS
1. Solve the simultaneous equations:
a) $y = 6 - x$
$x^2 + y^2 = 20$ [4]
b) $y = x - 5$
$y = x^2 - 5x - 12$](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FhispBneKVjQVSLLYjXJf_image_page_3.webp&w=2048&q=75)
![SIMULTANEOUS EQUATIONS
1. Solve the simultaneous equations:
a) $y = 6 - x$
$x^2 + y^2 = 20$ [4]
b) $y = x - 5$
$y = x^2 - 5x - 12$](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FhispBneKVjQVSLLYjXJf_image_page_4.webp&w=2048&q=75)
![SIMULTANEOUS EQUATIONS
1. Solve the simultaneous equations:
a) $y = 6 - x$
$x^2 + y^2 = 20$ [4]
b) $y = x - 5$
$y = x^2 - 5x - 12$](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FhispBneKVjQVSLLYjXJf_image_page_5.webp&w=2048&q=75)
![SIMULTANEOUS EQUATIONS
1. Solve the simultaneous equations:
a) $y = 6 - x$
$x^2 + y^2 = 20$ [4]
b) $y = x - 5$
$y = x^2 - 5x - 12$](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2FhispBneKVjQVSLLYjXJf_image_page_6.webp&w=2048&q=75)