Maths can feel overwhelming with all its different topics, but... Show more
Sign up to see the contentIt's free!
Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Subjects
Classic Dramatic Literature
Modern Lyric Poetry
Influential English-Language Authors
Classic and Contemporary Novels
Literary Character Analysis
Romantic and Love Poetry
Reading Analysis and Interpretation
Evidence Analysis and Integration
Author's Stylistic Elements
Figurative Language and Rhetoric
Show all topics
Human Organ Systems
Cellular Organization and Development
Biomolecular Structure and Organization
Enzyme Structure and Regulation
Cellular Organization Types
Biological Homeostatic Processes
Cellular Membrane Structure
Autotrophic Energy Processes
Environmental Sustainability and Impact
Neural Communication Systems
Show all topics
Social Sciences Research & Practice
Social Structure and Mobility
Classic Social Influence Experiments
Social Systems Theories
Family and Relationship Dynamics
Memory Systems and Processes
Neural Bases of Behavior
Social Influence and Attraction
Psychotherapeutic Approaches
Human Agency and Responsibility
Show all topics
Chemical Sciences and Applications
Chemical Bond Types and Properties
Organic Functional Groups
Atomic Structure and Composition
Chromatographic Separation Principles
Chemical Compound Classifications
Electrochemical Cell Systems
Periodic Table Organization
Chemical Reaction Kinetics
Chemical Equation Conservation
Show all topics
Nazi Germany and Holocaust 1933-1945
World Wars and Peace Treaties
European Monarchs and Statesmen
Cold War Global Tensions
Medieval Institutions and Systems
European Renaissance and Enlightenment
Modern Global Environmental-Health Challenges
Modern Military Conflicts
Medieval Migration and Invasions
World Wars Era and Impact
Show all topics
170
•
11 Feb 2026
•
Charlotte
@charlotte26
Maths can feel overwhelming with all its different topics, but... Show more
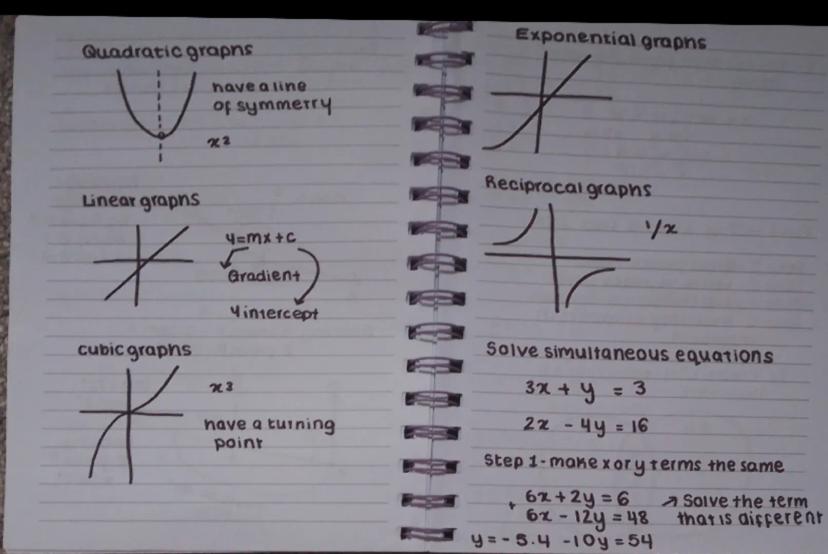









Understanding different graph shapes is crucial for recognising functions at a glance. Linear graphs follow the pattern y = mx + c, where m is the gradient and c is the y-intercept. Quadratic graphs (containing x²) create U-shaped curves with a line of symmetry, whilst cubic graphs (containing x³) have distinctive S-shapes with turning points.
Exponential graphs show rapid growth or decay, and reciprocal graphs create hyperbolas that never touch the axes. Each graph type has its own unique characteristics that help you identify the underlying equation.
When solving simultaneous equations like 3x + y = 3 and 2x - 4y = 16, start by making either the x or y terms the same. Multiply the first equation by 2 to get matching x terms: 6x + 2y = 6 and 6x - 12y = 48. Then subtract to eliminate x and solve for the remaining variable.
Quick tip: Always check your answer by substituting both values back into the original equations!

After eliminating one variable in simultaneous equations, substitute your answer back into either original equation. If you found y = -4, plug it into 3x + y = 3 to get 3x + (-4) = 3, giving you x = 2.8. This systematic approach works every time.
Finding the HCF (Highest Common Factor) of numbers like 84 and 140 involves drawing factor trees, then using a Venn diagram to identify common factors. The HCF is found by multiplying the numbers in the intersection - in this case, 28. For the LCM (Lowest Common Multiple), you'd multiply all the numbers instead.
Index laws might look scary, but they follow clear patterns. Remember that anything to the power of 0 equals 1, fractional powers mean roots , and negative powers create fractions . For mixed powers like 25^(3/2), find the root first , then apply the other power (5³ = 125).
Remember: Index laws are just shortcuts for repeated multiplication and division!

Calculating the estimated mean from grouped data requires finding midpoints for each interval. Multiply each midpoint by its frequency, add all these products together, then divide by the total frequency. For the height data shown, this gives 3936 ÷ 25 = 167.4 cm.
Combining ratios needs careful attention to make terms match. If a:b = 3:4 and b:c = 6:2, you need to make the 'b' values the same. Scale the ratios so both have b = 20, giving a:b:c = 15:20:8.
Sequences come in different types, each with distinct patterns. Linear sequences have constant differences , giving the formula 4n + 2. Quadratic sequences have differences that change by a constant amount - look for the second difference to spot these. Fibonacci sequences add the two previous terms together (3, 1, 4, 5, 9...).
Pattern spotting: Always look at the differences between terms first - they reveal the sequence type!

Geometric sequences multiply or divide by the same value each time. In the sequence 5, 5√3, 45, 45√3, you're multiplying by √3 each time. The nth term formula is a × r^, where 'a' is the first term and 'r' is the multiplier.
Direct proportion means as one variable increases, the other increases at the same rate (y ∝ x). The graph is a straight line through the origin. Inverse proportion means as one increases, the other decreases , creating a curved graph.
To find proportion formulas, use the given values to work out the constant 'k'. If y is directly proportional to x, and when x = 8, y = 40, then y = kx becomes 40 = 8k, so k = 5. Therefore y = 5x.
For inverse proportion like d ∝ 1/w², use d = k/w². If w = 0.5 and d = 12, then 12 = k/0.25, giving k = 3. So d = 3/w².
Proportion tip: Direct proportion gives straight-line graphs, inverse proportion gives curves!

Cumulative frequency tables build running totals by adding each frequency to the previous total. When plotting cumulative frequency graphs, always use the upper boundary of each class interval on the x-axis.
Finding quartiles from cumulative frequency is straightforward: the median is at ½ of the total frequency, the lower quartile (LQ) at ¼, and the upper quartile (UQ) at ¾. These values help you understand how data is spread out.
Histograms are different from bar charts because they show frequency density, not just frequency. Calculate frequency density using the formula: frequency ÷ class width. This ensures that areas of bars represent frequencies accurately, even when class widths vary.
The key to histogram success is remembering that area equals frequency. Wider bars need lower heights to represent the same frequency as narrower bars.
Data analysis: Always check whether you need frequency or frequency density - it makes a huge difference!

Angle facts form the foundation of geometry problem-solving. Triangle angles always add to 180°, whilst angles around a point total 360°. Quadrilateral angles also sum to 360°.
For polygons, the exterior angles always add up to 360°, regardless of the number of sides. The formula for total interior angles is × 180°, where n is the number of sides. Divide this by the number of sides to find each interior angle in a regular polygon.
Parallel line properties are essential for angle calculations. Corresponding angles are equal (in the same relative positions), alternate angles are equal (on opposite sides of the transversal), and co-interior angles add up to 180° (on the same side of the transversal).
Vertically opposite angles are always equal when two lines cross. These angle properties often combine in exam questions, so practise identifying multiple relationships in single diagrams.
Angle hunting: Look for parallel lines and transversals - they're goldmines for angle relationships!

Adding and subtracting fractions requires a common denominator. Convert mixed numbers to improper fractions first , find the lowest common multiple of denominators, then add or subtract the numerators.
Multiplying fractions is simpler - just multiply numerators together and denominators together, then simplify. For division, use 'Keep, Change, Flip': keep the first fraction, change ÷ to ×, and flip the second fraction upside down.
Converting recurring decimals to fractions uses algebra. For 0.3̄ (0.333...), let x = 0.333..., then 10x = 3.333.... Subtract to get 9x = 3, so x = ⅓. For longer recurring parts like 0.123̄, multiply by 1000 and 10 to create the equation 990x = 122.
The key is choosing the right powers of 10 based on how many digits recur. One recurring digit needs ×10, two digits need ×100, and so on.
Fraction wisdom: Always simplify your final answer - it often makes the numbers much friendlier!

Completing the square transforms quadratic expressions into a more useful form. Take x² + 8x + 6: halve the x-coefficient (8 ÷ 2 = 4), write as ², then adjust for the constant. Since ² = x² + 8x + 16, you need ² - 10 to get back to the original expression.
The turning point of a parabola comes directly from the completed square form. From ² - 10, the turning point is (-4, -10) - take the opposite sign of the first number and keep the second as is.
For expressions with coefficients of x², like 3x² + 18x - 1, factor out the coefficient first: 3 - 1, then complete the square inside the brackets.
Context problems involving direct and inverse proportion appear frequently. If 12 people take 5 hours to complete a job, that's 60 person-hours of work. With 15 people, the same job takes 60 ÷ 15 = 4 hours.
Proportion in context: Total work stays constant - more people means less time per person!

Algebraic fractions follow the same rules as number fractions but with algebra. Find common denominators for addition and subtraction, multiply straight across for multiplication, and use 'keep, change, flip' for division.
When solving equations with algebraic fractions, multiply through by the common denominator to eliminate fractions. For example, if 1/30x = 4, multiply both sides by 30x to get 1 = 120x, so x = 1/120.
Simplifying complex algebraic fractions often requires factorising first. Look for common factors in numerators and denominators that can cancel out.
Pythagoras' theorem finds missing sides in right-angled triangles. Remember that 'c' is always the longest side (hypotenuse). Square the two known sides, add or subtract as needed, then square root your answer.
Ratios in context require careful reading. If the total of some parts equals a given amount, find the value of one part by dividing, then multiply to find other parts.
Algebraic confidence: Treat algebraic fractions just like number fractions - the rules are identical!
Our AI Companion is a student-focused AI tool that offers more than just answers. Built on millions of Knowunity resources, it provides relevant information, personalised study plans, quizzes, and content directly in the chat, adapting to your individual learning journey.
You can download the app from Google Play Store and Apple App Store.
That's right! Enjoy free access to study content, connect with fellow students, and get instant help – all at your fingertips.
App Store
Google Play
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
Best app on earth! no words because it’s too good
Thomas R
iOS user
Just amazing. Let's me revise 10x better, this app is a quick 10/10. I highly recommend it to anyone. I can watch and search for notes. I can save them in the subject folder. I can revise it any time when I come back. If you haven't tried this app, you're really missing out.
Basil
Android user
This app has made me feel so much more confident in my exam prep, not only through boosting my own self confidence through the features that allow you to connect with others and feel less alone, but also through the way the app itself is centred around making you feel better. It is easy to navigate, fun to use, and helpful to anyone struggling in absolutely any way.
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
very reliable app to help and grow your ideas of Maths, English and other related topics in your works. please use this app if your struggling in areas, this app is key for that. wish I'd of done a review before. and it's also free so don't worry about that.
Rohan U
Android user
I know a lot of apps use fake accounts to boost their reviews but this app deserves it all. Originally I was getting 4 in my English exams and this time I got a grade 7. I didn’t even know about this app three days until the exam and it has helped A LOT. Please actually trust me and use it as I’m sure you too will see developments.
Xander S
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE Knowunity AI. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This apps acc the goat. I find revision so boring but this app makes it so easy to organize it all and then you can ask the freeeee ai to test yourself so good and you can easily upload your own stuff. highly recommend as someone taking mocks now
Paul T
iOS user
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
Best app on earth! no words because it’s too good
Thomas R
iOS user
Just amazing. Let's me revise 10x better, this app is a quick 10/10. I highly recommend it to anyone. I can watch and search for notes. I can save them in the subject folder. I can revise it any time when I come back. If you haven't tried this app, you're really missing out.
Basil
Android user
This app has made me feel so much more confident in my exam prep, not only through boosting my own self confidence through the features that allow you to connect with others and feel less alone, but also through the way the app itself is centred around making you feel better. It is easy to navigate, fun to use, and helpful to anyone struggling in absolutely any way.
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
very reliable app to help and grow your ideas of Maths, English and other related topics in your works. please use this app if your struggling in areas, this app is key for that. wish I'd of done a review before. and it's also free so don't worry about that.
Rohan U
Android user
I know a lot of apps use fake accounts to boost their reviews but this app deserves it all. Originally I was getting 4 in my English exams and this time I got a grade 7. I didn’t even know about this app three days until the exam and it has helped A LOT. Please actually trust me and use it as I’m sure you too will see developments.
Xander S
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE Knowunity AI. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This apps acc the goat. I find revision so boring but this app makes it so easy to organize it all and then you can ask the freeeee ai to test yourself so good and you can easily upload your own stuff. highly recommend as someone taking mocks now
Paul T
iOS user
Charlotte
@charlotte26
Maths can feel overwhelming with all its different topics, but breaking it down into bite-sized chunks makes everything much clearer. These notes cover the essential topics you'll need for your GCSE exams, from graphs and equations to fractions and geometry.

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Understanding different graph shapes is crucial for recognising functions at a glance. Linear graphs follow the pattern y = mx + c, where m is the gradient and c is the y-intercept. Quadratic graphs (containing x²) create U-shaped curves with a line of symmetry, whilst cubic graphs (containing x³) have distinctive S-shapes with turning points.
Exponential graphs show rapid growth or decay, and reciprocal graphs create hyperbolas that never touch the axes. Each graph type has its own unique characteristics that help you identify the underlying equation.
When solving simultaneous equations like 3x + y = 3 and 2x - 4y = 16, start by making either the x or y terms the same. Multiply the first equation by 2 to get matching x terms: 6x + 2y = 6 and 6x - 12y = 48. Then subtract to eliminate x and solve for the remaining variable.
Quick tip: Always check your answer by substituting both values back into the original equations!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
After eliminating one variable in simultaneous equations, substitute your answer back into either original equation. If you found y = -4, plug it into 3x + y = 3 to get 3x + (-4) = 3, giving you x = 2.8. This systematic approach works every time.
Finding the HCF (Highest Common Factor) of numbers like 84 and 140 involves drawing factor trees, then using a Venn diagram to identify common factors. The HCF is found by multiplying the numbers in the intersection - in this case, 28. For the LCM (Lowest Common Multiple), you'd multiply all the numbers instead.
Index laws might look scary, but they follow clear patterns. Remember that anything to the power of 0 equals 1, fractional powers mean roots , and negative powers create fractions . For mixed powers like 25^(3/2), find the root first , then apply the other power (5³ = 125).
Remember: Index laws are just shortcuts for repeated multiplication and division!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Calculating the estimated mean from grouped data requires finding midpoints for each interval. Multiply each midpoint by its frequency, add all these products together, then divide by the total frequency. For the height data shown, this gives 3936 ÷ 25 = 167.4 cm.
Combining ratios needs careful attention to make terms match. If a:b = 3:4 and b:c = 6:2, you need to make the 'b' values the same. Scale the ratios so both have b = 20, giving a:b:c = 15:20:8.
Sequences come in different types, each with distinct patterns. Linear sequences have constant differences , giving the formula 4n + 2. Quadratic sequences have differences that change by a constant amount - look for the second difference to spot these. Fibonacci sequences add the two previous terms together (3, 1, 4, 5, 9...).
Pattern spotting: Always look at the differences between terms first - they reveal the sequence type!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Geometric sequences multiply or divide by the same value each time. In the sequence 5, 5√3, 45, 45√3, you're multiplying by √3 each time. The nth term formula is a × r^, where 'a' is the first term and 'r' is the multiplier.
Direct proportion means as one variable increases, the other increases at the same rate (y ∝ x). The graph is a straight line through the origin. Inverse proportion means as one increases, the other decreases , creating a curved graph.
To find proportion formulas, use the given values to work out the constant 'k'. If y is directly proportional to x, and when x = 8, y = 40, then y = kx becomes 40 = 8k, so k = 5. Therefore y = 5x.
For inverse proportion like d ∝ 1/w², use d = k/w². If w = 0.5 and d = 12, then 12 = k/0.25, giving k = 3. So d = 3/w².
Proportion tip: Direct proportion gives straight-line graphs, inverse proportion gives curves!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Cumulative frequency tables build running totals by adding each frequency to the previous total. When plotting cumulative frequency graphs, always use the upper boundary of each class interval on the x-axis.
Finding quartiles from cumulative frequency is straightforward: the median is at ½ of the total frequency, the lower quartile (LQ) at ¼, and the upper quartile (UQ) at ¾. These values help you understand how data is spread out.
Histograms are different from bar charts because they show frequency density, not just frequency. Calculate frequency density using the formula: frequency ÷ class width. This ensures that areas of bars represent frequencies accurately, even when class widths vary.
The key to histogram success is remembering that area equals frequency. Wider bars need lower heights to represent the same frequency as narrower bars.
Data analysis: Always check whether you need frequency or frequency density - it makes a huge difference!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Angle facts form the foundation of geometry problem-solving. Triangle angles always add to 180°, whilst angles around a point total 360°. Quadrilateral angles also sum to 360°.
For polygons, the exterior angles always add up to 360°, regardless of the number of sides. The formula for total interior angles is × 180°, where n is the number of sides. Divide this by the number of sides to find each interior angle in a regular polygon.
Parallel line properties are essential for angle calculations. Corresponding angles are equal (in the same relative positions), alternate angles are equal (on opposite sides of the transversal), and co-interior angles add up to 180° (on the same side of the transversal).
Vertically opposite angles are always equal when two lines cross. These angle properties often combine in exam questions, so practise identifying multiple relationships in single diagrams.
Angle hunting: Look for parallel lines and transversals - they're goldmines for angle relationships!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Adding and subtracting fractions requires a common denominator. Convert mixed numbers to improper fractions first , find the lowest common multiple of denominators, then add or subtract the numerators.
Multiplying fractions is simpler - just multiply numerators together and denominators together, then simplify. For division, use 'Keep, Change, Flip': keep the first fraction, change ÷ to ×, and flip the second fraction upside down.
Converting recurring decimals to fractions uses algebra. For 0.3̄ (0.333...), let x = 0.333..., then 10x = 3.333.... Subtract to get 9x = 3, so x = ⅓. For longer recurring parts like 0.123̄, multiply by 1000 and 10 to create the equation 990x = 122.
The key is choosing the right powers of 10 based on how many digits recur. One recurring digit needs ×10, two digits need ×100, and so on.
Fraction wisdom: Always simplify your final answer - it often makes the numbers much friendlier!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Completing the square transforms quadratic expressions into a more useful form. Take x² + 8x + 6: halve the x-coefficient (8 ÷ 2 = 4), write as ², then adjust for the constant. Since ² = x² + 8x + 16, you need ² - 10 to get back to the original expression.
The turning point of a parabola comes directly from the completed square form. From ² - 10, the turning point is (-4, -10) - take the opposite sign of the first number and keep the second as is.
For expressions with coefficients of x², like 3x² + 18x - 1, factor out the coefficient first: 3 - 1, then complete the square inside the brackets.
Context problems involving direct and inverse proportion appear frequently. If 12 people take 5 hours to complete a job, that's 60 person-hours of work. With 15 people, the same job takes 60 ÷ 15 = 4 hours.
Proportion in context: Total work stays constant - more people means less time per person!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Algebraic fractions follow the same rules as number fractions but with algebra. Find common denominators for addition and subtraction, multiply straight across for multiplication, and use 'keep, change, flip' for division.
When solving equations with algebraic fractions, multiply through by the common denominator to eliminate fractions. For example, if 1/30x = 4, multiply both sides by 30x to get 1 = 120x, so x = 1/120.
Simplifying complex algebraic fractions often requires factorising first. Look for common factors in numerators and denominators that can cancel out.
Pythagoras' theorem finds missing sides in right-angled triangles. Remember that 'c' is always the longest side (hypotenuse). Square the two known sides, add or subtract as needed, then square root your answer.
Ratios in context require careful reading. If the total of some parts equals a given amount, find the value of one part by dividing, then multiply to find other parts.
Algebraic confidence: Treat algebraic fractions just like number fractions - the rules are identical!
Our AI Companion is a student-focused AI tool that offers more than just answers. Built on millions of Knowunity resources, it provides relevant information, personalised study plans, quizzes, and content directly in the chat, adapting to your individual learning journey.
You can download the app from Google Play Store and Apple App Store.
That's right! Enjoy free access to study content, connect with fellow students, and get instant help – all at your fingertips.
5
Smart Tools NEW
Transform this note into: ✓ 50+ Practice Questions ✓ Interactive Flashcards ✓ Full Mock Exam ✓ Essay Outlines
App Store
Google Play
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
Best app on earth! no words because it’s too good
Thomas R
iOS user
Just amazing. Let's me revise 10x better, this app is a quick 10/10. I highly recommend it to anyone. I can watch and search for notes. I can save them in the subject folder. I can revise it any time when I come back. If you haven't tried this app, you're really missing out.
Basil
Android user
This app has made me feel so much more confident in my exam prep, not only through boosting my own self confidence through the features that allow you to connect with others and feel less alone, but also through the way the app itself is centred around making you feel better. It is easy to navigate, fun to use, and helpful to anyone struggling in absolutely any way.
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
very reliable app to help and grow your ideas of Maths, English and other related topics in your works. please use this app if your struggling in areas, this app is key for that. wish I'd of done a review before. and it's also free so don't worry about that.
Rohan U
Android user
I know a lot of apps use fake accounts to boost their reviews but this app deserves it all. Originally I was getting 4 in my English exams and this time I got a grade 7. I didn’t even know about this app three days until the exam and it has helped A LOT. Please actually trust me and use it as I’m sure you too will see developments.
Xander S
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE Knowunity AI. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This apps acc the goat. I find revision so boring but this app makes it so easy to organize it all and then you can ask the freeeee ai to test yourself so good and you can easily upload your own stuff. highly recommend as someone taking mocks now
Paul T
iOS user
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
Best app on earth! no words because it’s too good
Thomas R
iOS user
Just amazing. Let's me revise 10x better, this app is a quick 10/10. I highly recommend it to anyone. I can watch and search for notes. I can save them in the subject folder. I can revise it any time when I come back. If you haven't tried this app, you're really missing out.
Basil
Android user
This app has made me feel so much more confident in my exam prep, not only through boosting my own self confidence through the features that allow you to connect with others and feel less alone, but also through the way the app itself is centred around making you feel better. It is easy to navigate, fun to use, and helpful to anyone struggling in absolutely any way.
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
very reliable app to help and grow your ideas of Maths, English and other related topics in your works. please use this app if your struggling in areas, this app is key for that. wish I'd of done a review before. and it's also free so don't worry about that.
Rohan U
Android user
I know a lot of apps use fake accounts to boost their reviews but this app deserves it all. Originally I was getting 4 in my English exams and this time I got a grade 7. I didn’t even know about this app three days until the exam and it has helped A LOT. Please actually trust me and use it as I’m sure you too will see developments.
Xander S
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE Knowunity AI. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This apps acc the goat. I find revision so boring but this app makes it so easy to organize it all and then you can ask the freeeee ai to test yourself so good and you can easily upload your own stuff. highly recommend as someone taking mocks now
Paul T
iOS user