Master Higher Maths: Comprehensive Revision Notes

Course Overview

This is your complete guide to CfE Higher Mathematics - the qualification that opens doors to university and beyond. These notes cover all the major topics you'll encounter throughout the year.

The content is organised into key areas that progressively build your mathematical skills. You'll start with coordinate geometry and work your way through to calculus concepts that form the basis of advanced mathematics.

Quick Tip: Keep these notes handy as a reference guide - they're designed to help you quickly find and understand the concepts you need most.

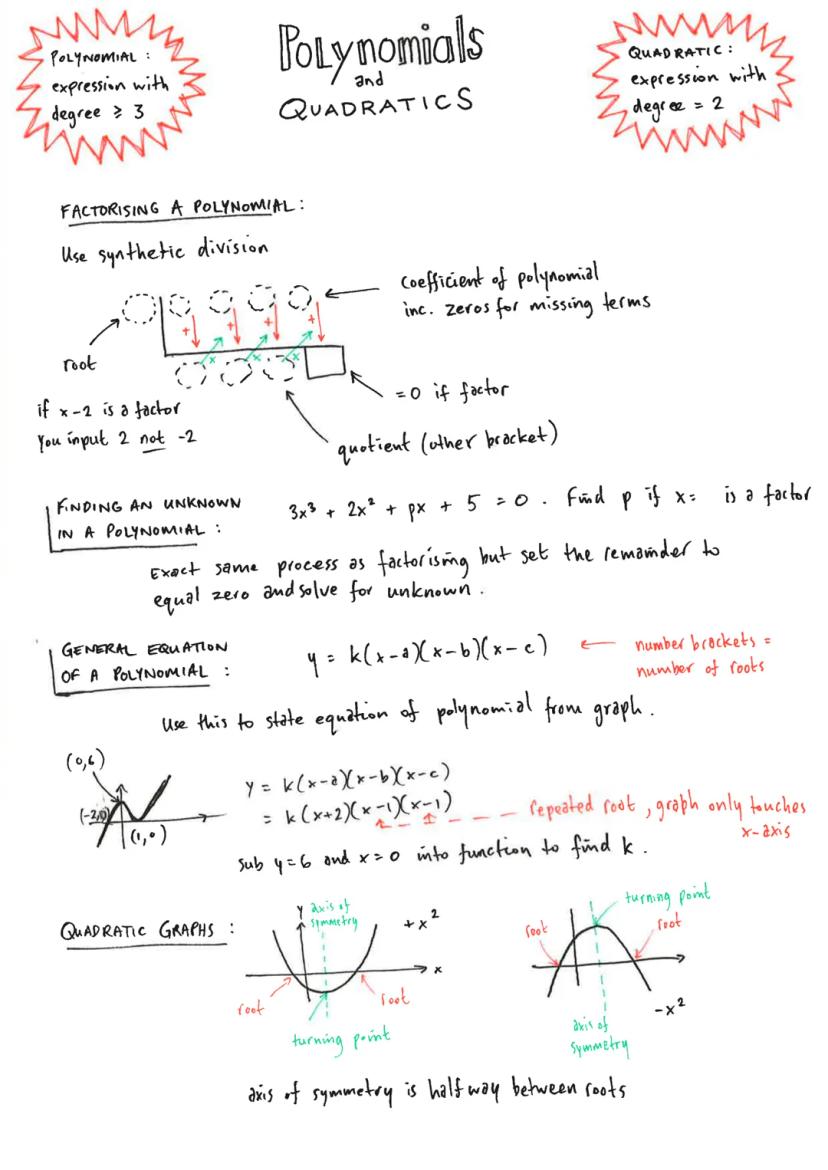
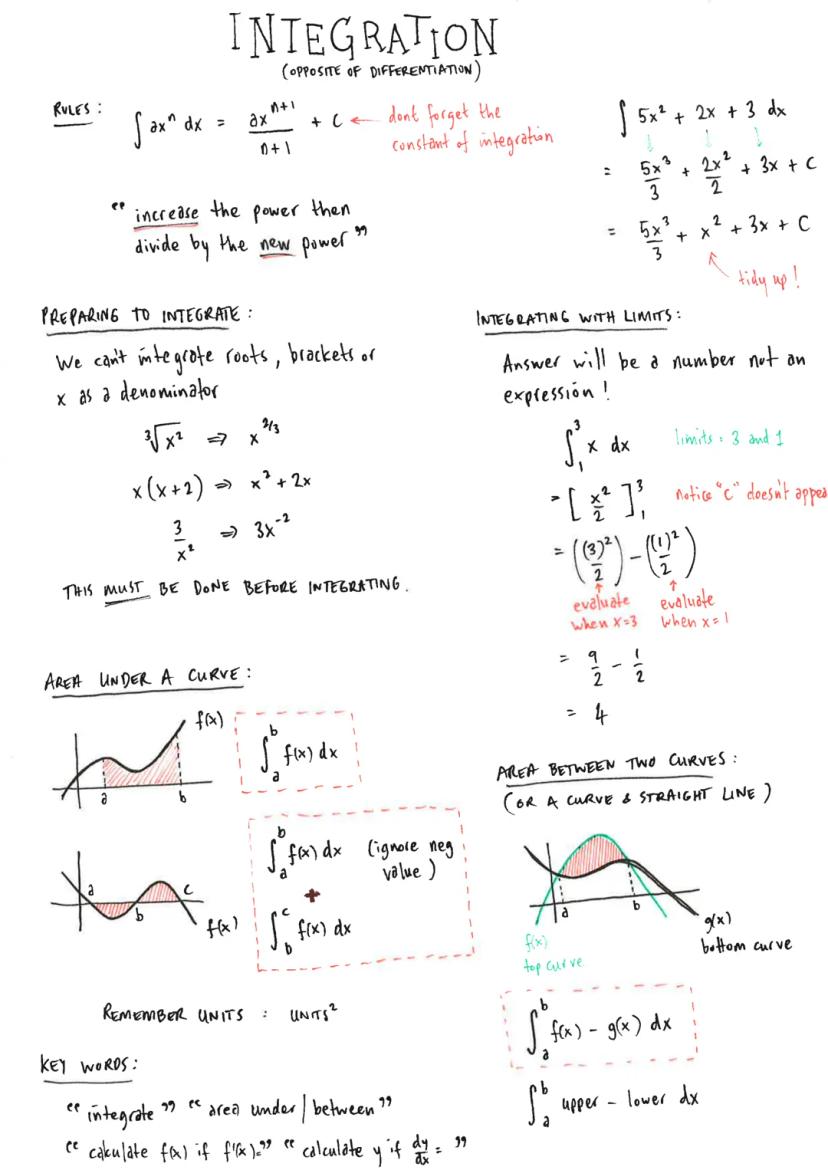
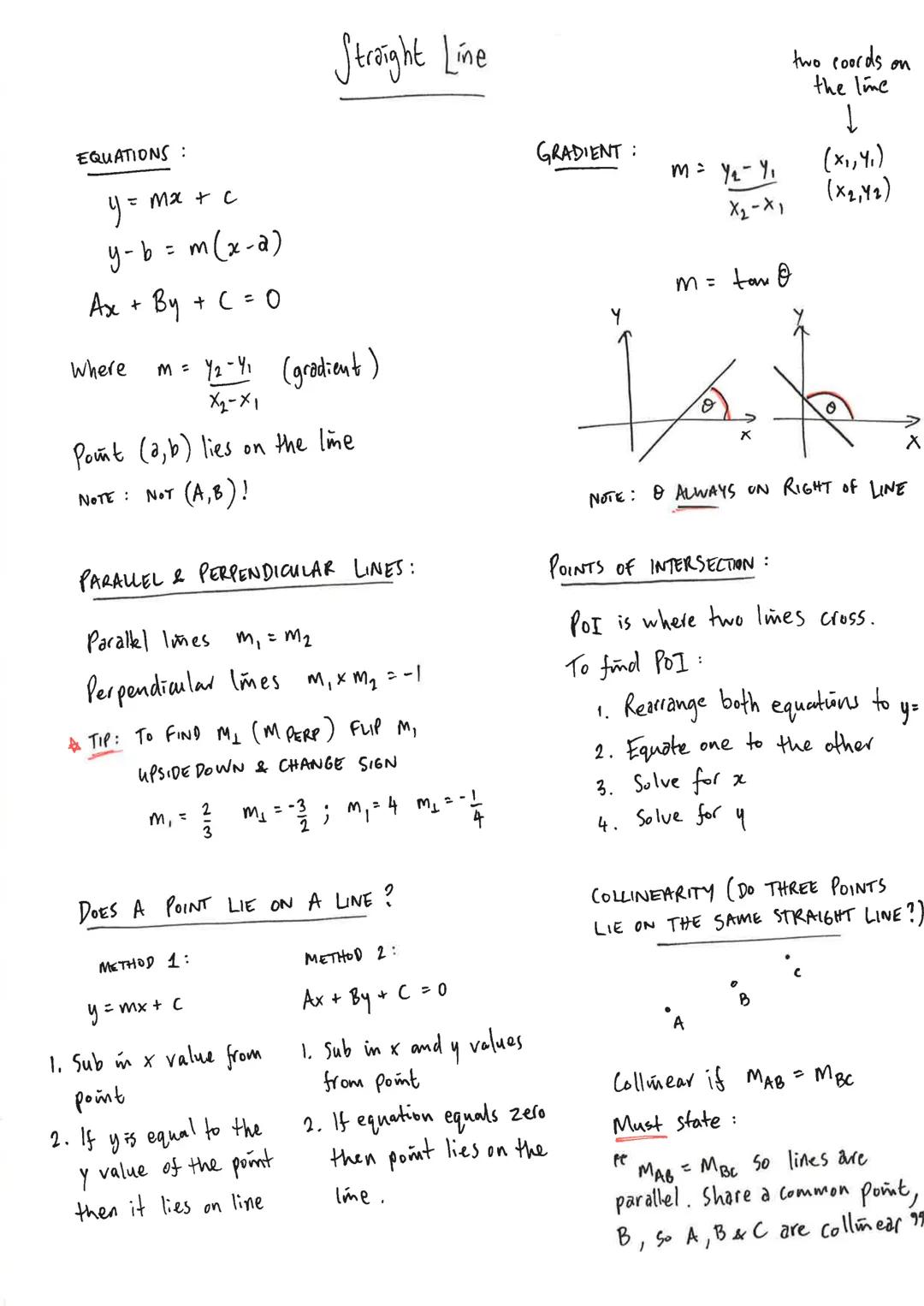
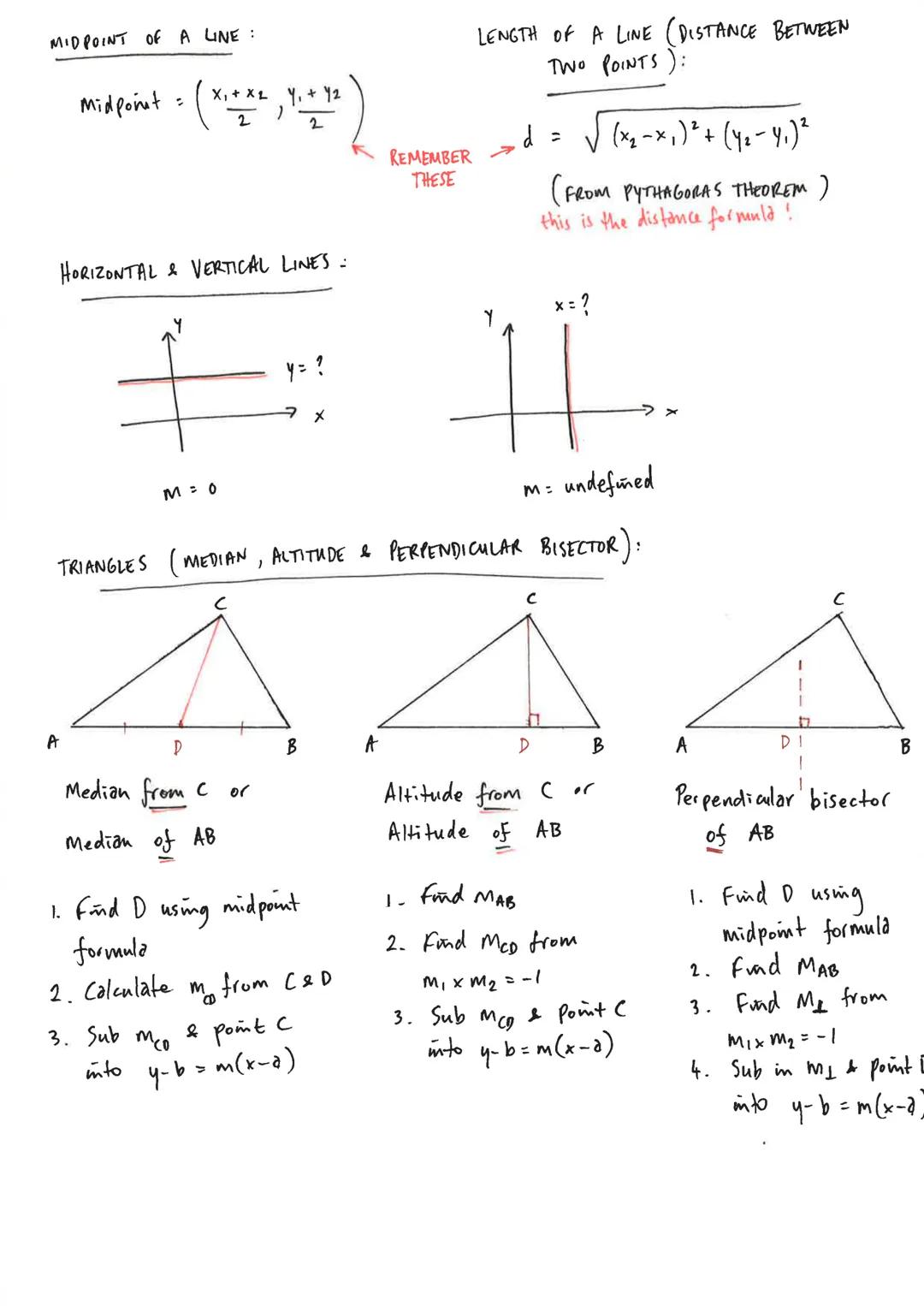
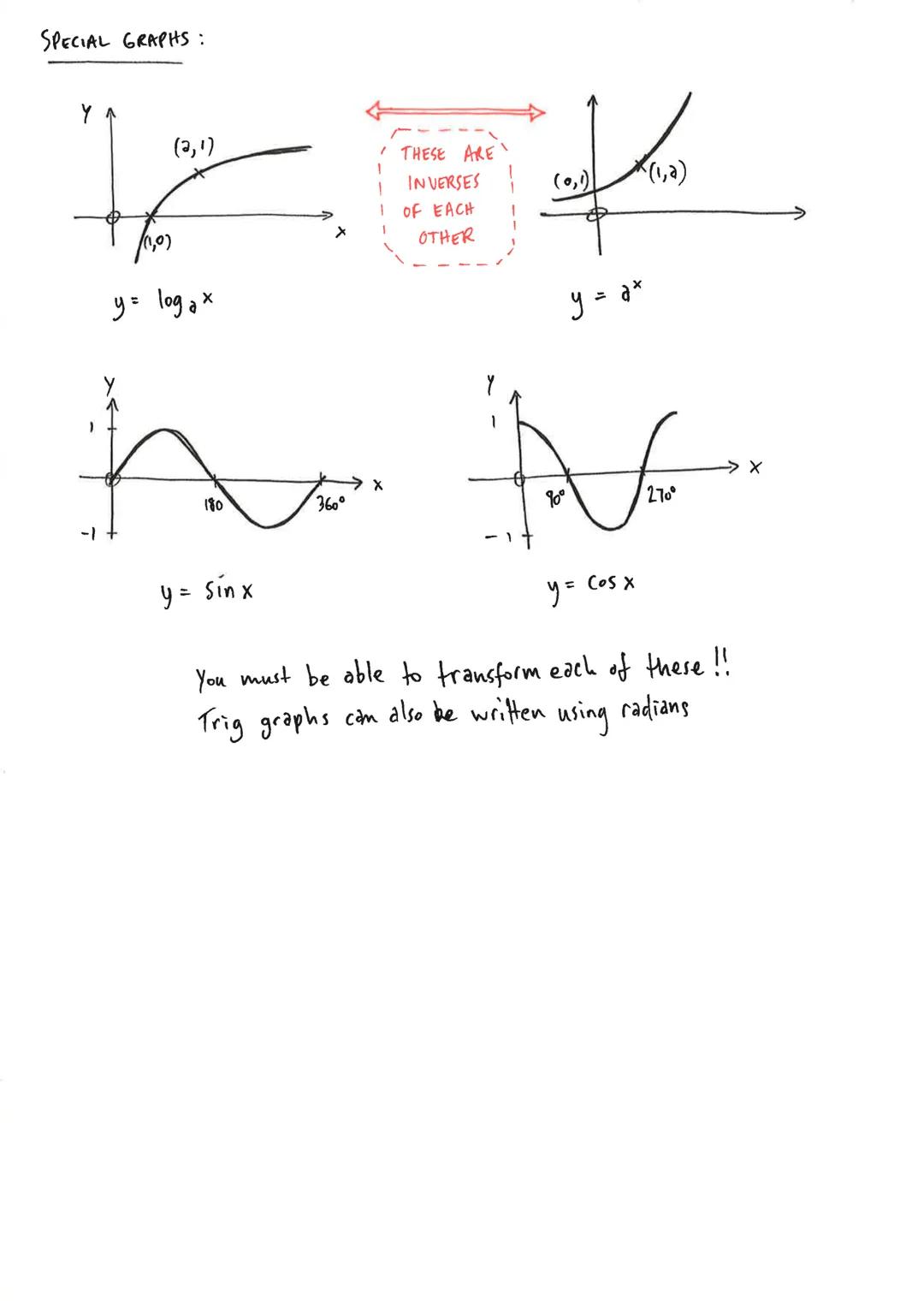
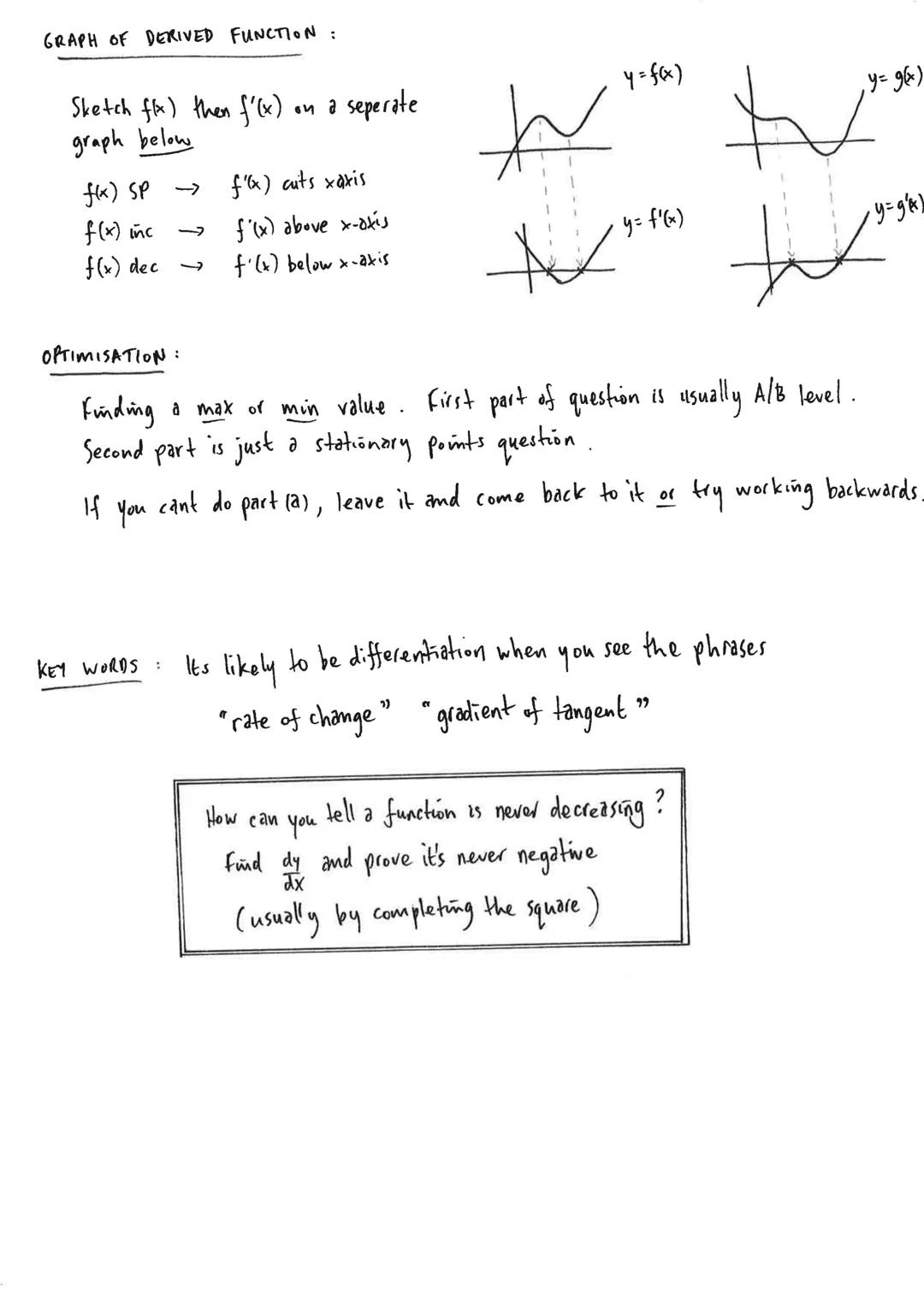
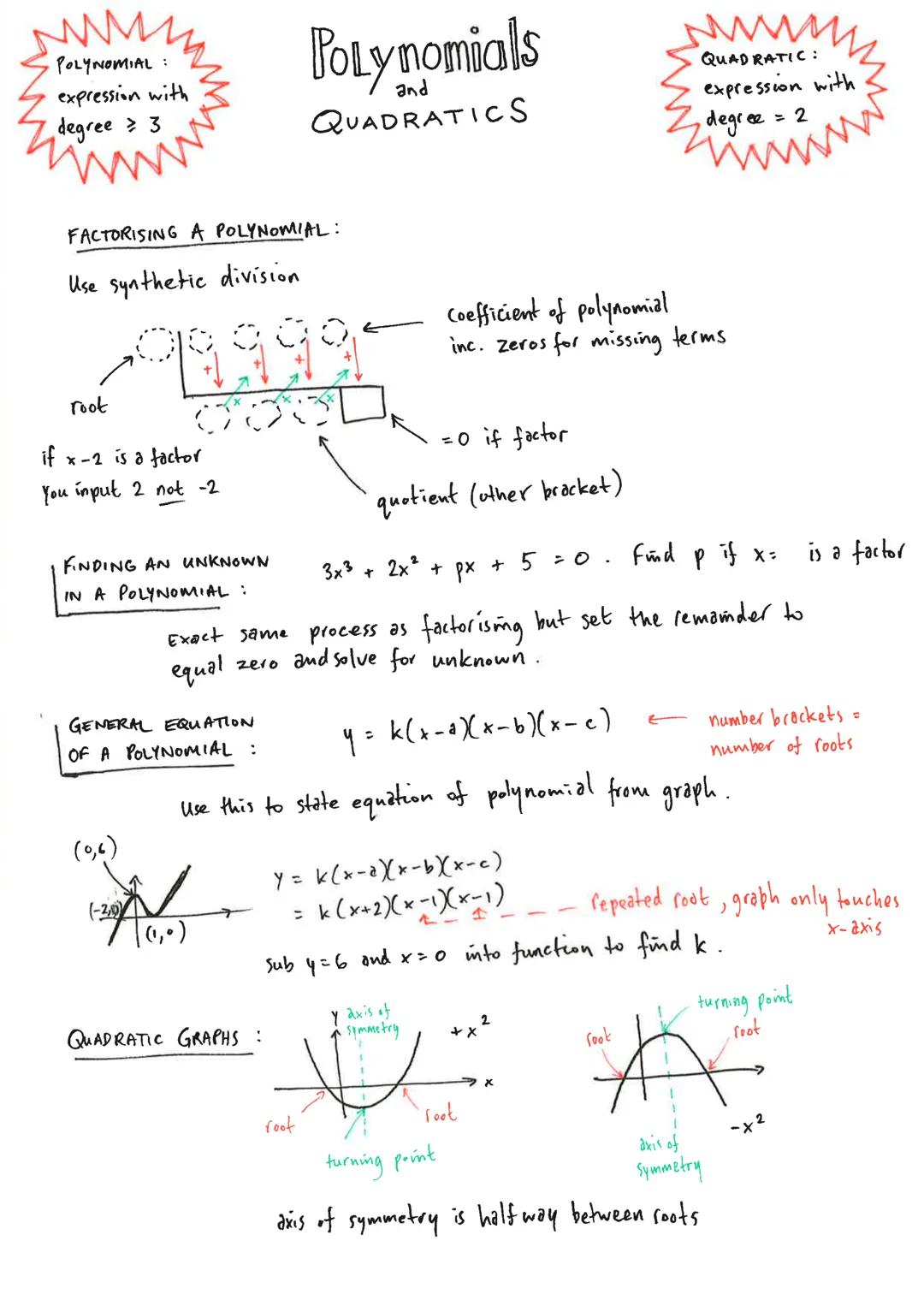
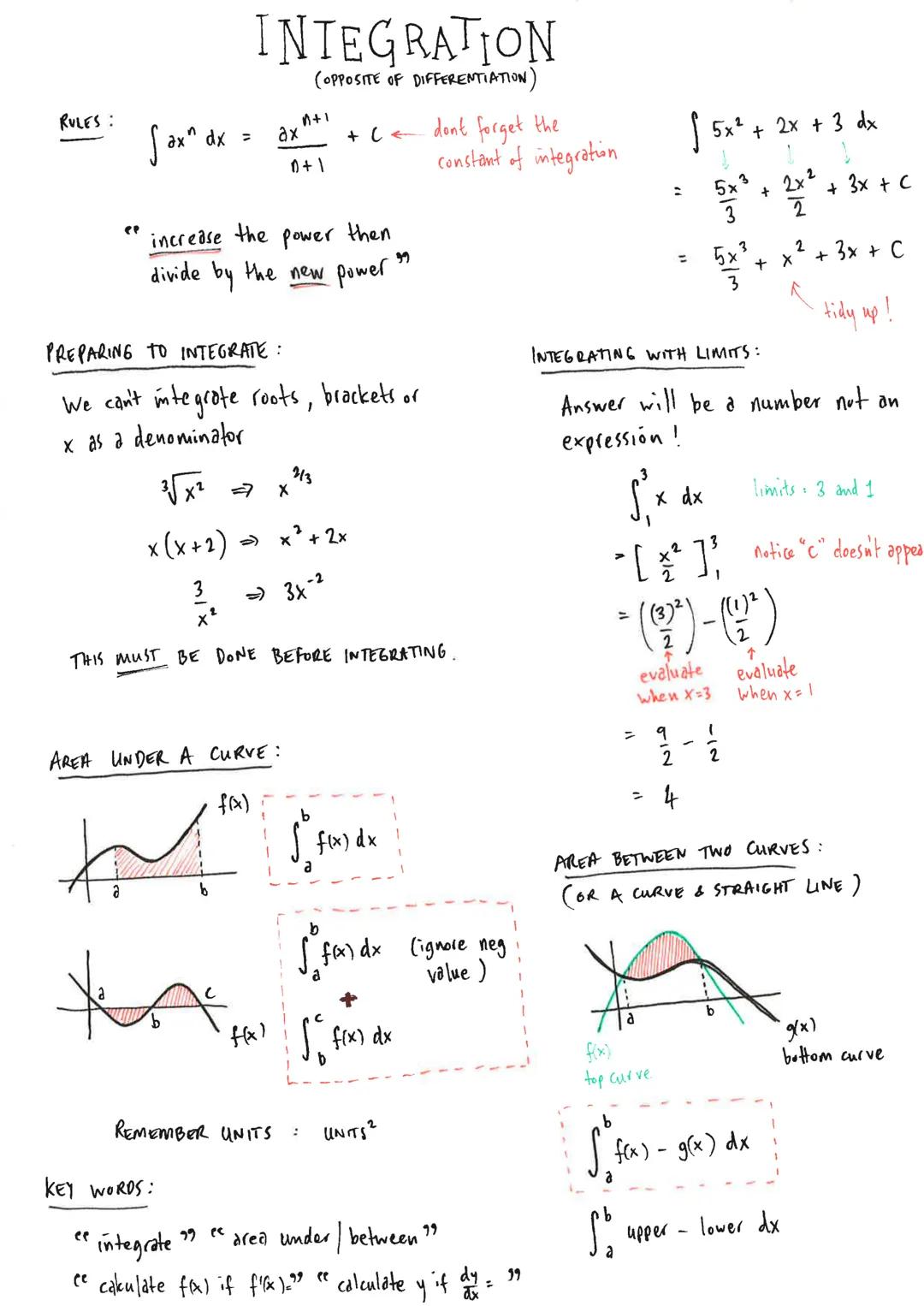
Straight Lines

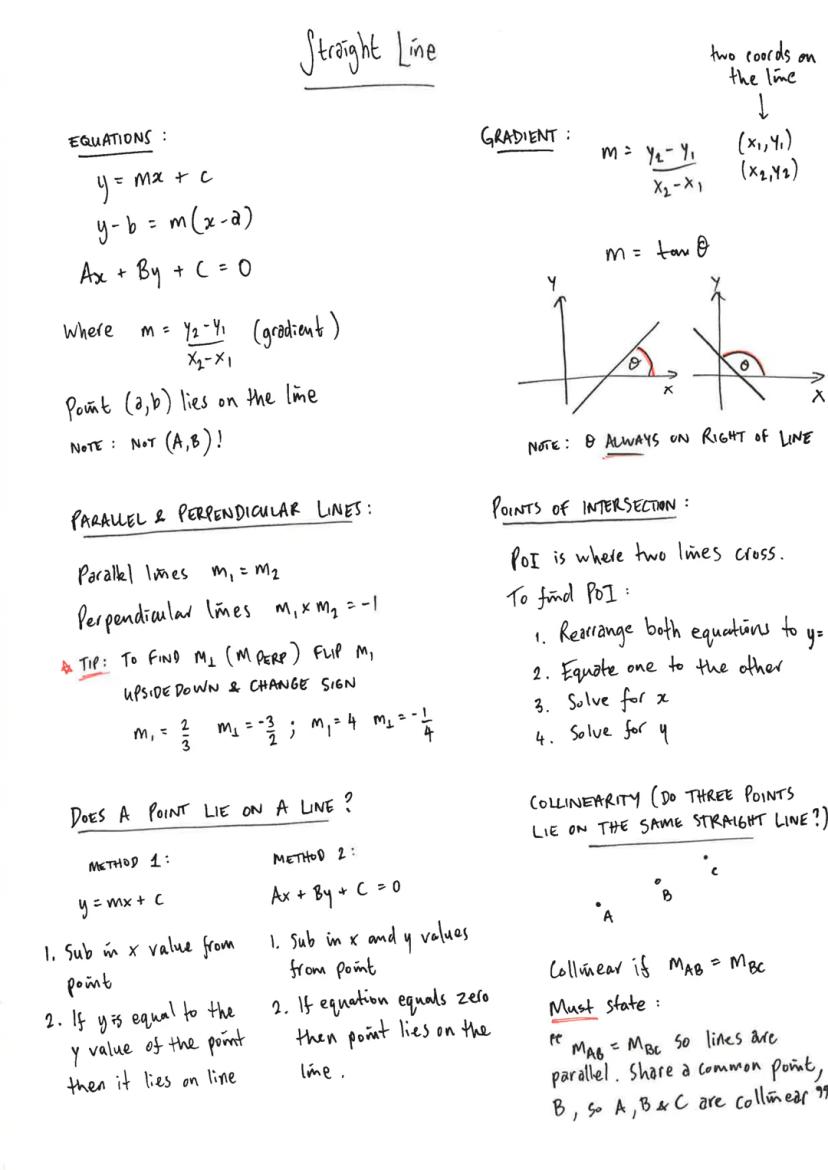
Want to master straight line equations? You've got three main forms to work with: y = mx + c, y - b = m$x - a$, and Ax + By + C = 0. The gradient formula m = $y₂ - y₁$/$x₂ - x₁$ is your best friend here.

Parallel and perpendicular lines follow simple rules. Parallel lines have identical gradients $m₁ = m₂$, whilst perpendicular lines multiply to give -1 $m₁ × m₂ = -1$. Here's a neat trick: to find a perpendicular gradient, flip the fraction upside down and change the sign.

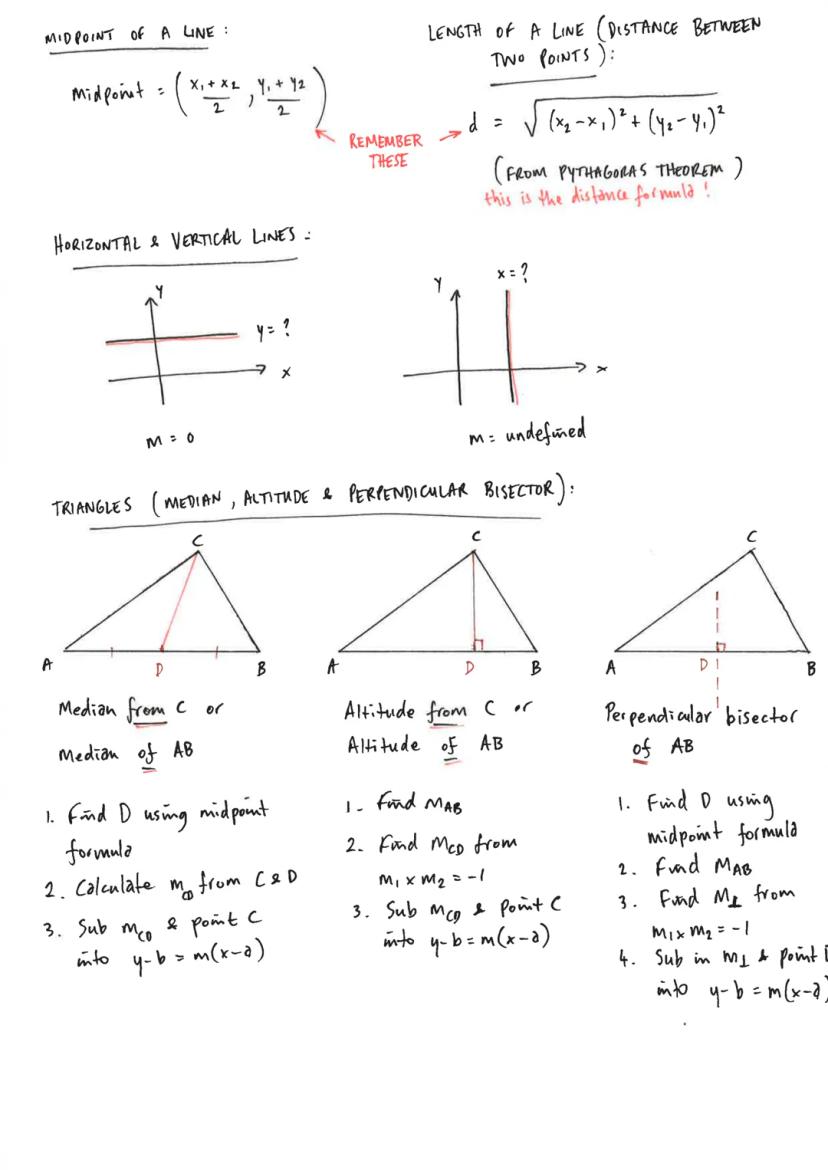
To check if a point lies on a line, substitute the coordinates into your equation. If it works out correctly, the point is on the line. For points of intersection, set your equations equal and solve - this is where two lines cross.

Collinearity (three points on the same line) requires you to prove that gradients between consecutive points are equal. Don't forget to state that the lines are parallel AND share a common point.

Exam Success: Always remember that θ (the angle) is measured from the positive x-axis, and it's always on the right side of your line.

Advanced Line Concepts

The midpoint formula $(x₁+x₂)/2, (y₁+y₂)/2$ and distance formula √$(x₂-x₁)² + (y₂-y₁)²$ are essential tools you'll use constantly. Think of the distance formula as Pythagoras' theorem in disguise.

Horizontal lines have gradient 0 (y = constant), whilst vertical lines have undefined gradient (x = constant). These special cases often catch students out in exams.

Triangle geometry involves three key concepts: medians (from vertex to midpoint), altitudes (perpendicular from vertex to opposite side), and perpendicular bisectors (perpendicular through the midpoint). Each follows a specific method, but they all use the same core principles of gradients and line equations.

Memory Aid: For triangle problems, always start by finding what you need first - whether it's a midpoint, a gradient, or a perpendicular gradient.

Functions and Graphs

Composite functions involve substituting one function into another - just work from the inside out! Remember that f(g$x$) ≠ g(f$x$) in most cases. When f(g$x$) = x, you've found inverse functions.

Restricted domains occur when you can't divide by zero or take the square root of negative numbers. Always check for these limitations in your functions.

Graph transformations follow predictable patterns. Adding to x-coordinates moves graphs horizontally (opposite to what you'd expect), whilst adding to y-coordinates moves them vertically. The "Miss Hunter method" gives you the complete rulebook.

For inverse functions, follow three steps: set f$x$ = y, rearrange to make x the subject, then swap x and y. The graphs of inverse functions are reflections of each other in the line y = x.

Transform Like a Pro: Changes inside the brackets affect x (horizontal), changes outside affect y (vertical). Remember that x-transformations work backwards!

Special Graphs

You must know these key graphs: exponential $y = aˣ$, logarithmic $y = log_a x$, sine $y = sin x$, and cosine $y = cos x$. The exponential and logarithmic functions are inverses of each other.

Trigonometric graphs have specific patterns you need to memorise. Sin x oscillates between -1 and 1, crossing zero at 0°, 180°, and 360°. Cos x also ranges from -1 to 1 but starts at its maximum value of 1 when x = 0°.

These graphs can be written using either degrees or radians - make sure you know which system you're working in. The transformation rules from the previous section apply to all these special graphs.

Graph Mastery: Practice sketching these from memory - they're the building blocks for more complex functions you'll encounter later.

Differentiation

Differentiation follows one main rule: f$x$ = axⁿ becomes f'$x$ = naxⁿ⁻¹. Multiply by the power, then decrease the power by one. Constants disappear completely.

Before differentiating, convert everything to index form. Roots become fractional powers, brackets must be expanded, and fractions become negative powers. This preparation is crucial.

Stationary points occur where f'$x$ = 0. Follow the six-step method: find f'$x$, set it to zero, solve for x, find y-coordinates, create a nature table, then state your answer with the nature of each point.

For tangent equations, you need the point of contact and the gradient at that point. The gradient of the tangent equals f'$x$ at any given x-value.

Differentiation Detective: Look for keywords like "rate of change" or "gradient of tangent" - these always signal differentiation questions.

Advanced Differentiation

Graphing derived functions requires understanding the relationship between f$x$ and f'$x$. Stationary points on f$x$ become x-intercepts on f'$x$. Where f$x$ increases, f'$x$ is positive (above the x-axis).

Optimisation problems often combine real-world scenarios with stationary point techniques. Don't panic if you can't complete part $a$ - attempt the differentiation in part $b$ anyway.

To prove a function is never decreasing, show that its derivative is never negative. This often involves completing the square to demonstrate the derivative is always ≥ 0.

Strategy Tip: In optimisation questions, the second part is usually just a standard stationary points question - focus your energy there if the setup is tricky.

Polynomials and Quadratics

Polynomials (degree ≥ 3) and quadratics (degree = 2) form the backbone of algebraic problem-solving. Use synthetic division to factorise polynomials when you know one factor.

Quadratic graphs are parabolas that either open upward (positive x²) or downward (negative x²). Key features include roots (x-intercepts), turning point (vertex), and axis of symmetry.

The general form y = kx-a$$x-b$$x-c shows you the roots directly. If a root appears twice, the graph only touches the x-axis at that point (repeated root).

Factorisation Focus: Synthetic division might look intimidating, but it's just organised long division - practice makes perfect!

Solving Quadratics

The discriminant $b² - 4ac$ tells you everything about quadratic roots. Positive means two real roots, zero means one real root (tangent), and negative means no real roots.

Solve quadratics by factorising or using the quadratic formula: x = $-b ± √(b² - 4ac)$/2a. Always include "x =" in your final answer.

Completing the square rewrites y = ax² + bx + c as y = a$x + p$² + q. This form immediately gives you the axis of symmetry $x = -p$ and turning point $-p, q$.

For tangent problems, set the curves equal, rearrange to standard form, then use the discriminant. When b² - 4ac = 0, you have exactly one point of contact.

Formula Power: Memorise the quadratic formula - it works every time, even when factorising seems impossible.

Integration

Integration reverses differentiation using the rule: ∫axⁿ dx = axⁿ⁺¹/$n+1$ + C. Increase the power, then divide by the new power. Never forget the constant C!

Like differentiation, preparation is key. Convert roots to fractional indices, expand brackets, and change fractions to negative powers before integrating.

Area under curves uses definite integration: ∫ᵇₐ f$x$ dx. When working with limits, substitute the upper limit minus the lower limit - no constant needed.

For area between curves, integrate the difference: ∫ᵇₐ (upper - lower) dx. Always consider which function is on top in your interval.

Integration Insight: Look for keywords like "area under," "area between," or "calculate f$x$ if f'$x$ = " - these signal integration problems.