Maths gets more exciting when you start combining calculus with... Show more
Sign up to see the contentIt's free!
Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Subjects
Classic Dramatic Literature
Modern Lyric Poetry
Influential English-Language Authors
Classic and Contemporary Novels
Literary Character Analysis
Romantic and Love Poetry
Reading Analysis and Interpretation
Evidence Analysis and Integration
Author's Stylistic Elements
Figurative Language and Rhetoric
Show all topics
Human Organ Systems
Cellular Organization and Development
Biomolecular Structure and Organization
Enzyme Structure and Regulation
Cellular Organization Types
Biological Homeostatic Processes
Cellular Membrane Structure
Autotrophic Energy Processes
Environmental Sustainability and Impact
Neural Communication Systems
Show all topics
Social Sciences Research & Practice
Social Structure and Mobility
Classic Social Influence Experiments
Social Systems Theories
Family and Relationship Dynamics
Memory Systems and Processes
Neural Bases of Behavior
Social Influence and Attraction
Psychotherapeutic Approaches
Human Agency and Responsibility
Show all topics
Chemical Sciences and Applications
Chemical Bond Types and Properties
Organic Functional Groups
Atomic Structure and Composition
Chromatographic Separation Principles
Chemical Compound Classifications
Electrochemical Cell Systems
Periodic Table Organization
Chemical Reaction Kinetics
Chemical Equation Conservation
Show all topics
Nazi Germany and Holocaust 1933-1945
World Wars and Peace Treaties
European Monarchs and Statesmen
Cold War Global Tensions
Medieval Institutions and Systems
European Renaissance and Enlightenment
Modern Global Environmental-Health Challenges
Modern Military Conflicts
Medieval Migration and Invasions
World Wars Era and Impact
Show all topics
249
•
7 Feb 2026
•
GNisha
@gnisha_fhdqlrplxiup
Maths gets more exciting when you start combining calculus with... Show more











You're about to dive into one of the most useful parts of A-level maths! Further calculus combines everything you know about differentiation and integration with trigonometric functions and composite functions.
This isn't just abstract maths - these techniques are essential for physics, engineering, and loads of real-world applications. Plus, they're guaranteed to appear on your exams, so getting comfortable with them now will pay off big time.
Quick tip: Always double-check your calculator is in radians mode when working with trig functions - this catches out loads of students!

Here's where calculus meets trigonometry! When you differentiate sin x and cos x, there are two simple rules that'll become second nature with practice.
For f(x) = sin ax, the derivative is f'(x) = a cos ax. For g(x) = cos ax, the derivative is g'(x) = -a sin ax. Notice that pesky minus sign with cosine - it trips up loads of students!
The key thing to remember is that you must always use radians when working with trig functions in calculus. When finding tangent equations, you'll need to find both the point on the curve and the gradient using these differentiation rules.
Remember: sin differentiates to cos, cos differentiates to -sin. The coefficient 'a' just tags along for the ride!

Things get more interesting when you have multiple trigonometric terms like f(x) = 2 sin x + 4 cos x. Just differentiate each term separately using your rules, so f'(x) = 2 cos x - 4 sin x.
For composite trig functions like sin, you need to multiply by the derivative of what's inside the brackets. So the derivative becomes 4cos.
This is actually a sneak preview of the chain rule, which you'll need for much more complex functions. The pattern is always the same: differentiate the outer function, then multiply by the derivative of the inner function.
Pro tip: When evaluating at specific values, substitute carefully and double-check your calculator is in radians mode!

The chain rule is your secret weapon for differentiating composite functions like f(g(x)). The formula is: d/dx [f(g(x))] = f'(g(x)) × g'(x).
Think of it as "differentiate the outside, leave the inside alone, then multiply by the derivative of the inside". For ⁴, you get 4³ × 3 = 12³.
It works brilliantly with trig functions too. For 3sin⁵x, treat it as 3(sin x)⁵. The derivative becomes 15(sin x)⁴ × cos x = 15cos x sin⁴x. Even square roots become manageable when you write them as fractional powers!
Chain rule mantra: Outside derivative × inside derivative. Say it until it's automatic!

The chain rule handles even the trickiest functions once you get the hang of it. For something like f(x) = 1/⁴, rewrite it as ⁻⁴ and apply the rule normally.
Fractional powers like ∛ become much easier when you write them as ^(5/3). Then it's just a case of bringing down the power, reducing it by one, and multiplying by the derivative of the bracket contents.
The key is recognising the pattern in every problem. Whether it's negative powers, fractional powers, or complex brackets, the chain rule approach stays exactly the same.
Success strategy: Always rewrite complex expressions using index notation first - it makes the chain rule much clearer!

Integration of trig functions follows two key rules that are the reverse of differentiation. ∫ sin ax dx = -1/a cos ax + C, and ∫ cos ax dx = 1/a sin ax + C.
Notice the negative sign when integrating sin x - this is the opposite of what happens with differentiation. For expressions with multiple terms like , just integrate each part separately.
Definite integrals work the same way, but remember to substitute your limits carefully and keep your calculator in radians mode. The fundamental theorem of calculus means you evaluate at the upper limit minus the lower limit.
Memory trick: Integration is differentiation backwards, so sin goes to -cos, and cos goes to sin!
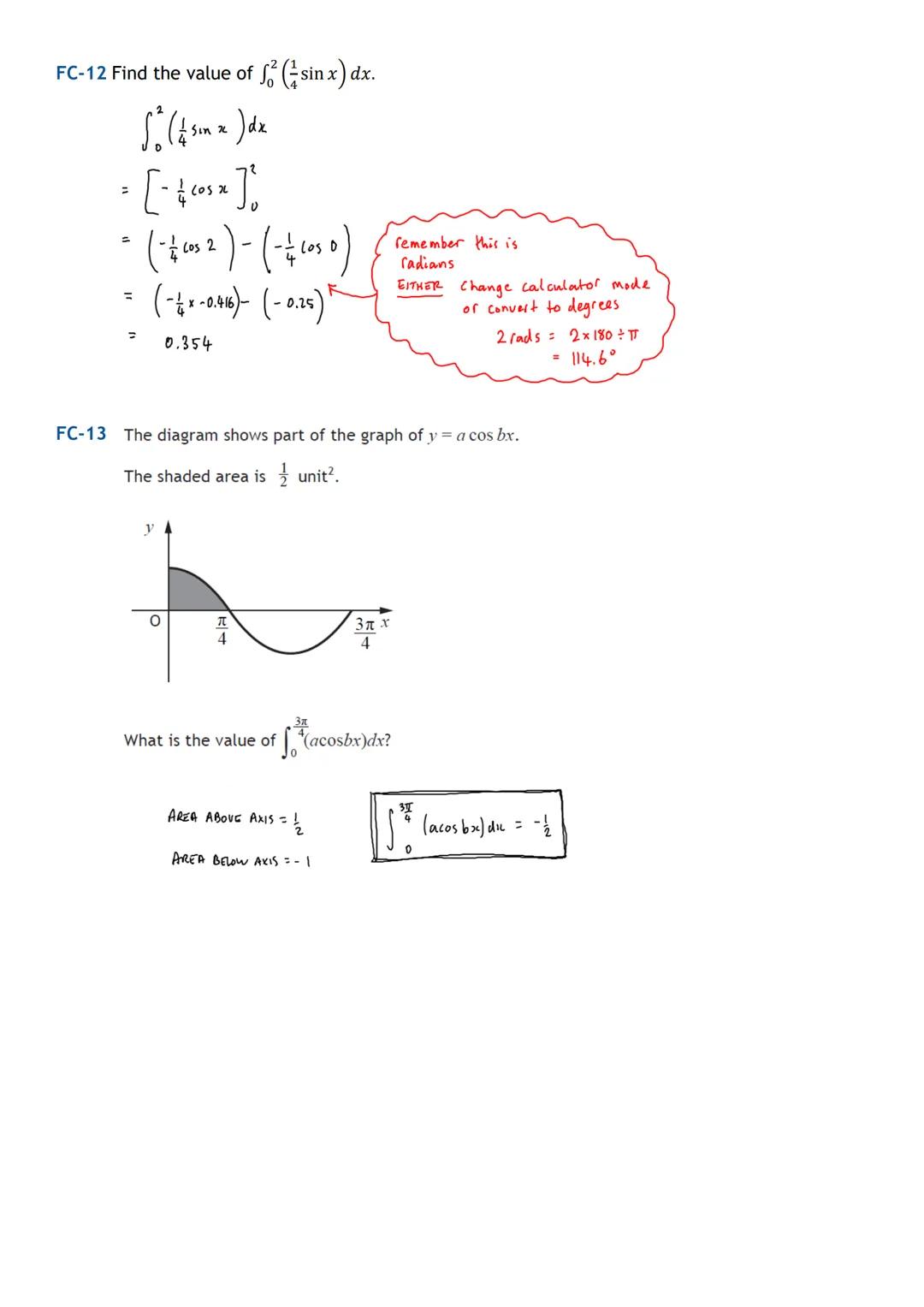
Definite integrals with trig functions can represent areas under curves, but watch out for negative areas! When a curve dips below the x-axis, the integral gives you a negative value.
For ∫₀^(π/2) dx, you get evaluated from 0 to π/2. This equals (-1/4 × 0) - (-1/4 × 1) = 1/4. Always double-check you're working in radians - converting 2 radians to degrees gives about 114.6°.
Sometimes you'll need to interpret area problems where the shaded region gives you information about the integral's value. If an area above the axis is 1/2 and below is -1, then the total integral equals -1/2.
Calculator check: When in doubt, verify your radian calculations by converting to degrees and back!

The special integral rule for ⁿ is incredibly useful: ∫ⁿ dx = ^/ + C. You increase the power by one, divide by the new power, then divide by the coefficient of x.
For something like ∫⁶ dx, you get ⁷/7 + C. When there's a coefficient like in ∫⁵ dx, don't forget to divide by that 4, giving you ⁶/24 + C.
Fractional and negative powers work exactly the same way. For ∫1/√ dx, rewrite it as ∫^(-1/2) dx, then apply the rule to get √/2 + C.
Golden rule: Increase the power by 1, divide by the new power, divide by the coefficient of x. Works every time!

Definite integrals with the special rule follow the same pattern, but require careful substitution of limits. For ∫₀³ 1/√ dx, first rewrite as ∫₀³ ^(-3/2) dx.
Apply the rule to get /(-1/2) × 1/3, which simplifies to [-2]/. Then substitute your limits: x = 3 gives -2/(3√16) = -1/6, and x = 0 gives -2/(3√7).
The final answer is the upper limit value minus the lower limit value. These calculations can get messy, so take your time and double-check each step - especially when dealing with negative fractional powers.
Stay organised: Write out each substitution step clearly. Rushing through limit calculations is where most errors happen!

This is one of the cleverest techniques in calculus! Sometimes you can use differentiation to help with integration by working backwards from a known derivative.
If you know that d/dx = x/√, then you can immediately see that ∫ x/√ dx must equal √ + C. This reverse engineering approach saves tons of time.
For ∫ 4x/√ dx, you just need to adjust for the coefficient 4, giving you 4√ + C. This technique is particularly useful when you spot that the numerator is related to the derivative of what's under the square root.
Pattern spotting: Always look for connections between the numerator and the derivative of the denominator - it's often the key to quick solutions!
Our AI Companion is a student-focused AI tool that offers more than just answers. Built on millions of Knowunity resources, it provides relevant information, personalised study plans, quizzes, and content directly in the chat, adapting to your individual learning journey.
You can download the app from Google Play Store and Apple App Store.
That's right! Enjoy free access to study content, connect with fellow students, and get instant help – all at your fingertips.
App Store
Google Play
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
Best app on earth! no words because it’s too good
Thomas R
iOS user
Just amazing. Let's me revise 10x better, this app is a quick 10/10. I highly recommend it to anyone. I can watch and search for notes. I can save them in the subject folder. I can revise it any time when I come back. If you haven't tried this app, you're really missing out.
Basil
Android user
This app has made me feel so much more confident in my exam prep, not only through boosting my own self confidence through the features that allow you to connect with others and feel less alone, but also through the way the app itself is centred around making you feel better. It is easy to navigate, fun to use, and helpful to anyone struggling in absolutely any way.
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
very reliable app to help and grow your ideas of Maths, English and other related topics in your works. please use this app if your struggling in areas, this app is key for that. wish I'd of done a review before. and it's also free so don't worry about that.
Rohan U
Android user
I know a lot of apps use fake accounts to boost their reviews but this app deserves it all. Originally I was getting 4 in my English exams and this time I got a grade 7. I didn’t even know about this app three days until the exam and it has helped A LOT. Please actually trust me and use it as I’m sure you too will see developments.
Xander S
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE Knowunity AI. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This apps acc the goat. I find revision so boring but this app makes it so easy to organize it all and then you can ask the freeeee ai to test yourself so good and you can easily upload your own stuff. highly recommend as someone taking mocks now
Paul T
iOS user
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
Best app on earth! no words because it’s too good
Thomas R
iOS user
Just amazing. Let's me revise 10x better, this app is a quick 10/10. I highly recommend it to anyone. I can watch and search for notes. I can save them in the subject folder. I can revise it any time when I come back. If you haven't tried this app, you're really missing out.
Basil
Android user
This app has made me feel so much more confident in my exam prep, not only through boosting my own self confidence through the features that allow you to connect with others and feel less alone, but also through the way the app itself is centred around making you feel better. It is easy to navigate, fun to use, and helpful to anyone struggling in absolutely any way.
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
very reliable app to help and grow your ideas of Maths, English and other related topics in your works. please use this app if your struggling in areas, this app is key for that. wish I'd of done a review before. and it's also free so don't worry about that.
Rohan U
Android user
I know a lot of apps use fake accounts to boost their reviews but this app deserves it all. Originally I was getting 4 in my English exams and this time I got a grade 7. I didn’t even know about this app three days until the exam and it has helped A LOT. Please actually trust me and use it as I’m sure you too will see developments.
Xander S
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE Knowunity AI. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This apps acc the goat. I find revision so boring but this app makes it so easy to organize it all and then you can ask the freeeee ai to test yourself so good and you can easily upload your own stuff. highly recommend as someone taking mocks now
Paul T
iOS user
GNisha
@gnisha_fhdqlrplxiup
Maths gets more exciting when you start combining calculus with trigonometry! This guide covers the essential skills for differentiating and integrating trig functions, plus some powerful techniques like the chain rule and special integrals that'll make you feel like a... Show more

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
You're about to dive into one of the most useful parts of A-level maths! Further calculus combines everything you know about differentiation and integration with trigonometric functions and composite functions.
This isn't just abstract maths - these techniques are essential for physics, engineering, and loads of real-world applications. Plus, they're guaranteed to appear on your exams, so getting comfortable with them now will pay off big time.
Quick tip: Always double-check your calculator is in radians mode when working with trig functions - this catches out loads of students!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Here's where calculus meets trigonometry! When you differentiate sin x and cos x, there are two simple rules that'll become second nature with practice.
For f(x) = sin ax, the derivative is f'(x) = a cos ax. For g(x) = cos ax, the derivative is g'(x) = -a sin ax. Notice that pesky minus sign with cosine - it trips up loads of students!
The key thing to remember is that you must always use radians when working with trig functions in calculus. When finding tangent equations, you'll need to find both the point on the curve and the gradient using these differentiation rules.
Remember: sin differentiates to cos, cos differentiates to -sin. The coefficient 'a' just tags along for the ride!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Things get more interesting when you have multiple trigonometric terms like f(x) = 2 sin x + 4 cos x. Just differentiate each term separately using your rules, so f'(x) = 2 cos x - 4 sin x.
For composite trig functions like sin, you need to multiply by the derivative of what's inside the brackets. So the derivative becomes 4cos.
This is actually a sneak preview of the chain rule, which you'll need for much more complex functions. The pattern is always the same: differentiate the outer function, then multiply by the derivative of the inner function.
Pro tip: When evaluating at specific values, substitute carefully and double-check your calculator is in radians mode!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
The chain rule is your secret weapon for differentiating composite functions like f(g(x)). The formula is: d/dx [f(g(x))] = f'(g(x)) × g'(x).
Think of it as "differentiate the outside, leave the inside alone, then multiply by the derivative of the inside". For ⁴, you get 4³ × 3 = 12³.
It works brilliantly with trig functions too. For 3sin⁵x, treat it as 3(sin x)⁵. The derivative becomes 15(sin x)⁴ × cos x = 15cos x sin⁴x. Even square roots become manageable when you write them as fractional powers!
Chain rule mantra: Outside derivative × inside derivative. Say it until it's automatic!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
The chain rule handles even the trickiest functions once you get the hang of it. For something like f(x) = 1/⁴, rewrite it as ⁻⁴ and apply the rule normally.
Fractional powers like ∛ become much easier when you write them as ^(5/3). Then it's just a case of bringing down the power, reducing it by one, and multiplying by the derivative of the bracket contents.
The key is recognising the pattern in every problem. Whether it's negative powers, fractional powers, or complex brackets, the chain rule approach stays exactly the same.
Success strategy: Always rewrite complex expressions using index notation first - it makes the chain rule much clearer!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Integration of trig functions follows two key rules that are the reverse of differentiation. ∫ sin ax dx = -1/a cos ax + C, and ∫ cos ax dx = 1/a sin ax + C.
Notice the negative sign when integrating sin x - this is the opposite of what happens with differentiation. For expressions with multiple terms like , just integrate each part separately.
Definite integrals work the same way, but remember to substitute your limits carefully and keep your calculator in radians mode. The fundamental theorem of calculus means you evaluate at the upper limit minus the lower limit.
Memory trick: Integration is differentiation backwards, so sin goes to -cos, and cos goes to sin!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Definite integrals with trig functions can represent areas under curves, but watch out for negative areas! When a curve dips below the x-axis, the integral gives you a negative value.
For ∫₀^(π/2) dx, you get evaluated from 0 to π/2. This equals (-1/4 × 0) - (-1/4 × 1) = 1/4. Always double-check you're working in radians - converting 2 radians to degrees gives about 114.6°.
Sometimes you'll need to interpret area problems where the shaded region gives you information about the integral's value. If an area above the axis is 1/2 and below is -1, then the total integral equals -1/2.
Calculator check: When in doubt, verify your radian calculations by converting to degrees and back!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
The special integral rule for ⁿ is incredibly useful: ∫ⁿ dx = ^/ + C. You increase the power by one, divide by the new power, then divide by the coefficient of x.
For something like ∫⁶ dx, you get ⁷/7 + C. When there's a coefficient like in ∫⁵ dx, don't forget to divide by that 4, giving you ⁶/24 + C.
Fractional and negative powers work exactly the same way. For ∫1/√ dx, rewrite it as ∫^(-1/2) dx, then apply the rule to get √/2 + C.
Golden rule: Increase the power by 1, divide by the new power, divide by the coefficient of x. Works every time!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Definite integrals with the special rule follow the same pattern, but require careful substitution of limits. For ∫₀³ 1/√ dx, first rewrite as ∫₀³ ^(-3/2) dx.
Apply the rule to get /(-1/2) × 1/3, which simplifies to [-2]/. Then substitute your limits: x = 3 gives -2/(3√16) = -1/6, and x = 0 gives -2/(3√7).
The final answer is the upper limit value minus the lower limit value. These calculations can get messy, so take your time and double-check each step - especially when dealing with negative fractional powers.
Stay organised: Write out each substitution step clearly. Rushing through limit calculations is where most errors happen!

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
This is one of the cleverest techniques in calculus! Sometimes you can use differentiation to help with integration by working backwards from a known derivative.
If you know that d/dx = x/√, then you can immediately see that ∫ x/√ dx must equal √ + C. This reverse engineering approach saves tons of time.
For ∫ 4x/√ dx, you just need to adjust for the coefficient 4, giving you 4√ + C. This technique is particularly useful when you spot that the numerator is related to the derivative of what's under the square root.
Pattern spotting: Always look for connections between the numerator and the derivative of the denominator - it's often the key to quick solutions!
Our AI Companion is a student-focused AI tool that offers more than just answers. Built on millions of Knowunity resources, it provides relevant information, personalised study plans, quizzes, and content directly in the chat, adapting to your individual learning journey.
You can download the app from Google Play Store and Apple App Store.
That's right! Enjoy free access to study content, connect with fellow students, and get instant help – all at your fingertips.
4
Smart Tools NEW
Transform this note into: ✓ 50+ Practice Questions ✓ Interactive Flashcards ✓ Full Mock Exam ✓ Essay Outlines
App Store
Google Play
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
Best app on earth! no words because it’s too good
Thomas R
iOS user
Just amazing. Let's me revise 10x better, this app is a quick 10/10. I highly recommend it to anyone. I can watch and search for notes. I can save them in the subject folder. I can revise it any time when I come back. If you haven't tried this app, you're really missing out.
Basil
Android user
This app has made me feel so much more confident in my exam prep, not only through boosting my own self confidence through the features that allow you to connect with others and feel less alone, but also through the way the app itself is centred around making you feel better. It is easy to navigate, fun to use, and helpful to anyone struggling in absolutely any way.
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
very reliable app to help and grow your ideas of Maths, English and other related topics in your works. please use this app if your struggling in areas, this app is key for that. wish I'd of done a review before. and it's also free so don't worry about that.
Rohan U
Android user
I know a lot of apps use fake accounts to boost their reviews but this app deserves it all. Originally I was getting 4 in my English exams and this time I got a grade 7. I didn’t even know about this app three days until the exam and it has helped A LOT. Please actually trust me and use it as I’m sure you too will see developments.
Xander S
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE Knowunity AI. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This apps acc the goat. I find revision so boring but this app makes it so easy to organize it all and then you can ask the freeeee ai to test yourself so good and you can easily upload your own stuff. highly recommend as someone taking mocks now
Paul T
iOS user
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
Best app on earth! no words because it’s too good
Thomas R
iOS user
Just amazing. Let's me revise 10x better, this app is a quick 10/10. I highly recommend it to anyone. I can watch and search for notes. I can save them in the subject folder. I can revise it any time when I come back. If you haven't tried this app, you're really missing out.
Basil
Android user
This app has made me feel so much more confident in my exam prep, not only through boosting my own self confidence through the features that allow you to connect with others and feel less alone, but also through the way the app itself is centred around making you feel better. It is easy to navigate, fun to use, and helpful to anyone struggling in absolutely any way.
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
very reliable app to help and grow your ideas of Maths, English and other related topics in your works. please use this app if your struggling in areas, this app is key for that. wish I'd of done a review before. and it's also free so don't worry about that.
Rohan U
Android user
I know a lot of apps use fake accounts to boost their reviews but this app deserves it all. Originally I was getting 4 in my English exams and this time I got a grade 7. I didn’t even know about this app three days until the exam and it has helped A LOT. Please actually trust me and use it as I’m sure you too will see developments.
Xander S
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE Knowunity AI. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This apps acc the goat. I find revision so boring but this app makes it so easy to organize it all and then you can ask the freeeee ai to test yourself so good and you can easily upload your own stuff. highly recommend as someone taking mocks now
Paul T
iOS user