Completing the Square and the Quadratic Formula

Ever wondered where the quadratic formula actually comes from? It's not just magic - it's derived using completing the square, and once you understand this connection, quadratic equations become much less intimidating.

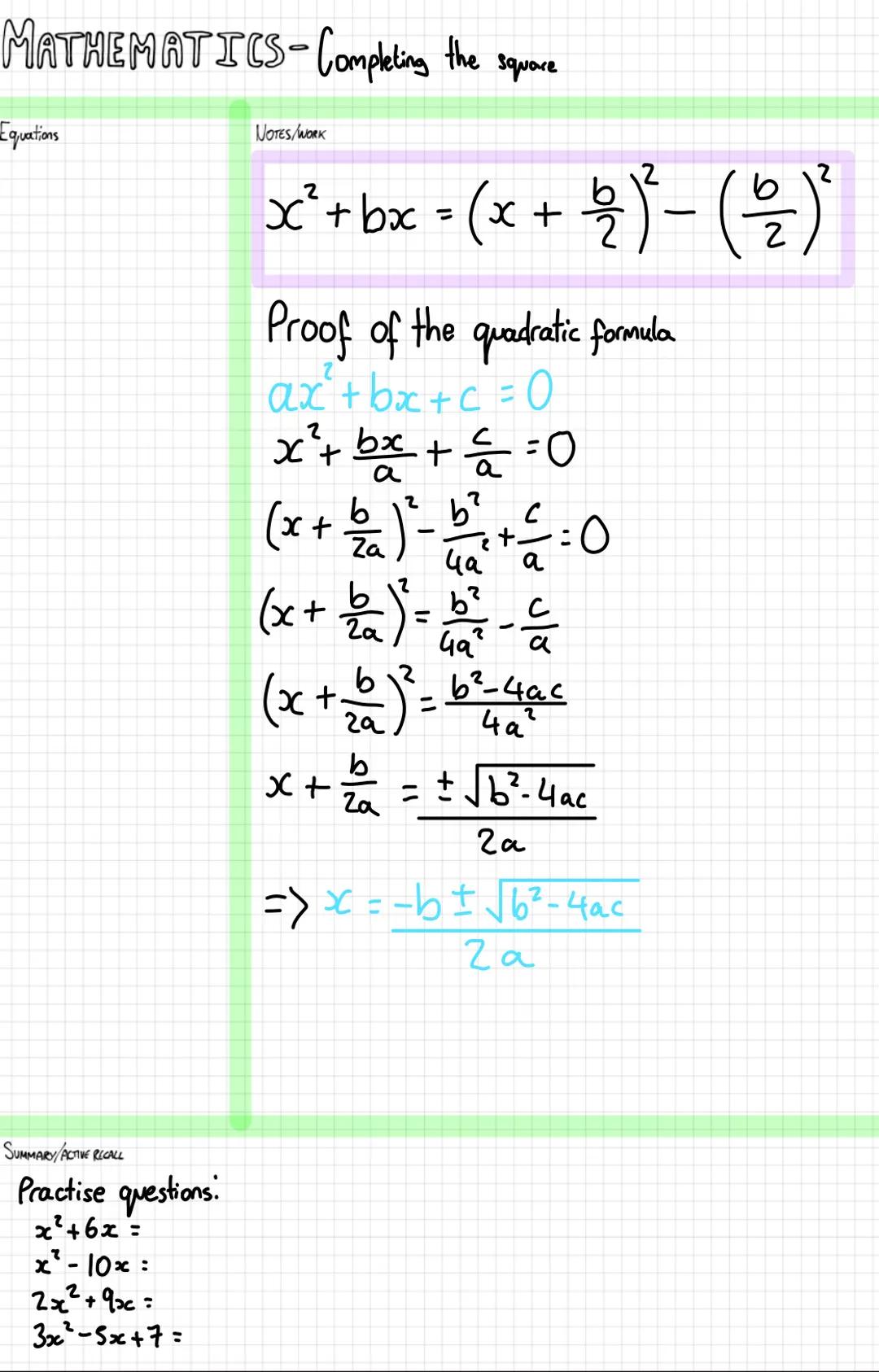
The basic pattern for completing the square is: x² + bx = $x + b/2$² - $b/2$². This formula lets you turn any quadratic expression into a perfect square plus or minus a constant. The key is taking half of the coefficient of x, squaring it, and both adding and subtracting it.

To prove the quadratic formula, we start with ax² + bx + c = 0 and divide everything by 'a' to get x² + (b/a)x + c/a = 0. Then we complete the square by adding $b/2a$² to both sides, which gives us $x + b/2a$² = $b² - 4ac$/4a². Taking the square root and rearranging leads directly to the familiar formula: x = $-b ± √(b² - 4ac)$/2a.

The practice questions show different types: simple cases like x² + 6x and x² - 10x, plus trickier ones where you need to factor out coefficients first, like 2x² + 9x and 3x² - 5x + 7.

Quick Tip: Always remember to halve the coefficient of x, then square that result - this is the number you add and subtract when completing the square.