Subjects

Careers

Open the App

Subjects

Subjects

Maths

Circles

Inscribed Angles

422

•

3 Mar 2023

•

5 pages

Circle Theorems Explained: Rules, Examples & Answer PDFs for Class 9 & 10

user profile picture

Shaz

@shaz2007

Circle Theorems: A Comprehensive Guide for Students

This guide provides... Show more

Circle Theorems Rule 1: Rule 2: A D Rute 3: Tangent meets Radius at 90° -B (Tangents that meet at a point are equal in length AB=BC The two

Additional Circle Theorem: Perpendicular to Chord

This page introduces an additional circle theorem rule that is crucial for solving more complex problems.

Definition: A perpendicular line from the center of a circle to a chord bisects the chord and forms right angles.

This theorem is particularly useful when dealing with problems involving chords and their relationships to the circle's center and circumference.

Highlight: Understanding this theorem can significantly simplify calculations in problems involving chord lengths and angles within circles.

Circle Theorems Rule 1: Rule 2: A D Rute 3: Tangent meets Radius at 90° -B (Tangents that meet at a point are equal in length AB=BC The two

Circle Theorem Questions: Practical Applications

This page presents a series of circle theorem questions and answers, demonstrating how to apply the rules in problem-solving scenarios.

  1. Question involving angles in the same segment: Given: Points A, B, C, and D on a circle Task: Find angle ACD Solution: ACD = 63° usingthe"bowtie"theoremusing the "bow tie" theorem
  2. Question on angles at the center and circumference: Given: Points A, B, C, and D on a circle with center O Tasks: Find angles x and y Solutions: x = 148° centerangletheoremcenter angle theorem, y = 106° cyclicquadrilateraltheoremcyclic quadrilateral theorem
  3. Complex question combining multiple theorems: Given: Circle with center O, tangent ABC, diameter BE Tasks: Find angles ABD and DEB Solutions: ABD = 54° tangent−radiustheoremtangent-radius theorem, DEB = 90° angleinsemicircletheoremangle in semicircle theorem

Example: In question 2, the solution demonstrates how angles at the center are twice the size of angles at the circumference, a key principle in circle theorems explained with examples.

Circle Theorems Rule 1: Rule 2: A D Rute 3: Tangent meets Radius at 90° -B (Tangents that meet at a point are equal in length AB=BC The two

Advanced Circle Theorem Problems

This page presents more challenging circle theorem questions, requiring the application of multiple rules and deeper analytical thinking.

  1. Problem involving isosceles triangles and tangents: Given: Circle with center O, points A, B, C, and tangent XCY Task: Find angle OCB Solution: OCB = 27° usingalternatesegmenttheoremandisoscelestrianglepropertiesusing alternate segment theorem and isosceles triangle properties
  2. Complex tangent problem: Given: Circle with center O, tangents PA and PB, angle APB = 86° Task: Find angle x Solution: x = 43° applyingmultipletheoremsincludingtangentpropertiesandisoscelestrianglesapplying multiple theorems including tangent properties and isosceles triangles

Highlight: These problems demonstrate how complex circle theorem problems and solutions often require a step-by-step approach, combining multiple theorems to reach the final answer.

Circle Theorems Rule 1: Rule 2: A D Rute 3: Tangent meets Radius at 90° -B (Tangents that meet at a point are equal in length AB=BC The two

Proof and Advanced Applications of Circle Theorems

This page focuses on proving circle theorems and solving highly complex problems, ideal for advanced students and GCSE circle theorems preparation.

  1. Proof question: Task: Prove that angle ROS = 2x, given RST = x Solution: Uses tangent-radius theorem, isosceles triangle properties, and angle sum theorems
  2. Advanced application question: Given: Circle with center O, tangent PT, straight line SOP, angle OPT = 32° Task: Find angle x Solution: x = 29° applyingmultipletheoremsandanglecalculationsapplying multiple theorems and angle calculations

Example: The proof question demonstrates how to construct a formal geometric proof using circle theorem rules, an essential skill for advanced mathematics.

Highlight: These problems are excellent practice for students preparing for difficult circle theorem questions and answers in exams.

Circle Theorems Rule 1: Rule 2: A D Rute 3: Tangent meets Radius at 90° -B (Tangents that meet at a point are equal in length AB=BC The two

Circle Theorems: Fundamental Rules and Applications

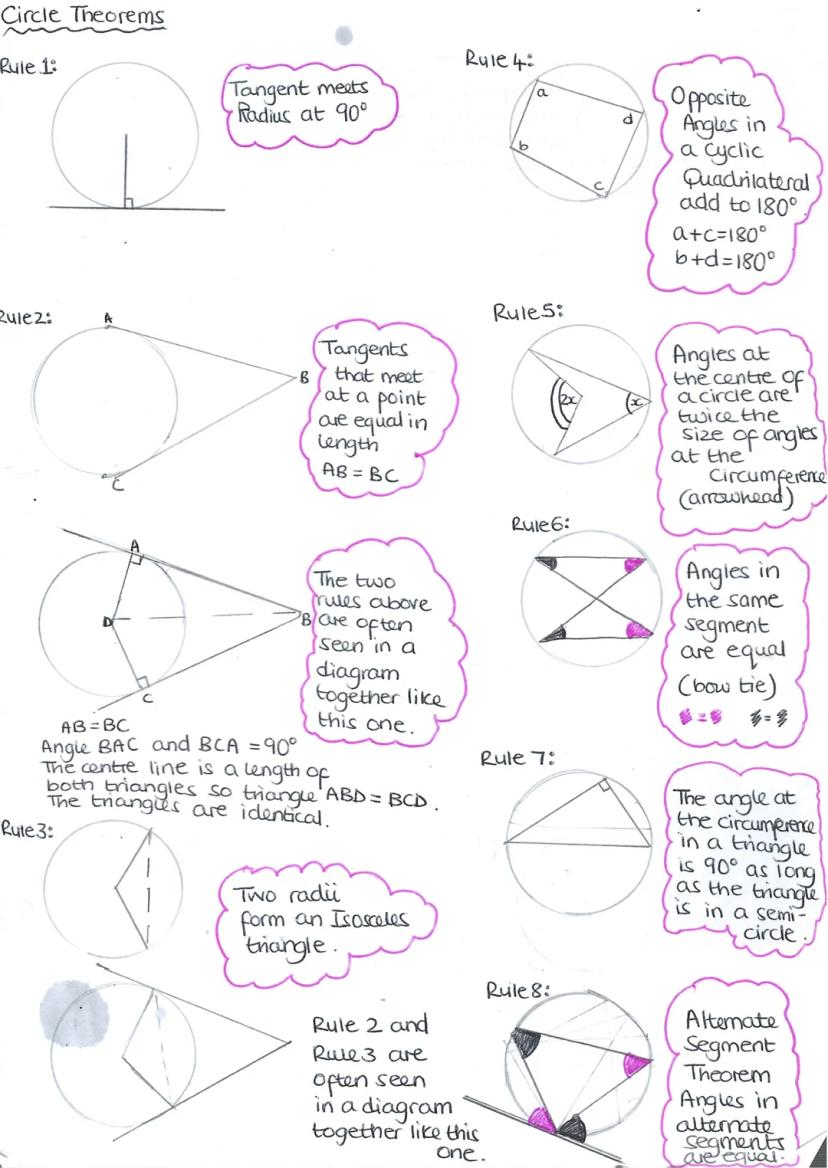
This page introduces eight essential circle theorem rules, providing a foundation for understanding geometric relationships within circles.

Definition: Circle theorems are geometric principles that describe relationships between angles, lines, and points in and around circles.

  1. Tangents meeting at a point are equal in length.
  2. A tangent meets a radius at a 90° angle.
  3. Two radii form an isosceles triangle.
  4. Opposite angles in a cyclic quadrilateral add up to 180°.
  5. The angle at the center is twice the size of the angle at the circumference.
  6. Angles in the same segment are equal.
  7. The angle at the circumference in a semicircle is 90°.
  8. Alternate segment theorem: Angles in alternate segments are equal.

Highlight: These rules are often combined in complex geometric problems, requiring students to apply multiple theorems simultaneously.

Example: Rule 2 and Rule 3 are frequently seen together in diagrams, where a tangent forms a right angle with a radius, and two radii create an isosceles triangle within the circle.



Can't find what you're looking for? Explore other subjects.

Students love us — and so will you.

4.9/5

App Store

4.8/5

Google Play

The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.

Stefan S

iOS user

This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.

Samantha Klich

Android user

Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.

Anna

iOS user

Best app on earth! no words because it’s too good

Thomas R

iOS user

Just amazing. Let's me revise 10x better, this app is a quick 10/10. I highly recommend it to anyone. I can watch and search for notes. I can save them in the subject folder. I can revise it any time when I come back. If you haven't tried this app, you're really missing out.

Basil

Android user

This app has made me feel so much more confident in my exam prep, not only through boosting my own self confidence through the features that allow you to connect with others and feel less alone, but also through the way the app itself is centred around making you feel better. It is easy to navigate, fun to use, and helpful to anyone struggling in absolutely any way.

David K

iOS user

The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!

Sudenaz Ocak

Android user

In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.

Greenlight Bonnie

Android user

very reliable app to help and grow your ideas of Maths, English and other related topics in your works. please use this app if your struggling in areas, this app is key for that. wish I'd of done a review before. and it's also free so don't worry about that.

Rohan U

Android user

I know a lot of apps use fake accounts to boost their reviews but this app deserves it all. Originally I was getting 4 in my English exams and this time I got a grade 7. I didn’t even know about this app three days until the exam and it has helped A LOT. Please actually trust me and use it as I’m sure you too will see developments.

Xander S

iOS user

THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE THE SCHOOLGPT. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮

Elisha

iOS user

This apps acc the goat. I find revision so boring but this app makes it so easy to organize it all and then you can ask the freeeee ai to test yourself so good and you can easily upload your own stuff. highly recommend as someone taking mocks now

Paul T

iOS user

The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.

Stefan S

iOS user

This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.

Samantha Klich

Android user

Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.

Anna

iOS user

Best app on earth! no words because it’s too good

Thomas R

iOS user

Just amazing. Let's me revise 10x better, this app is a quick 10/10. I highly recommend it to anyone. I can watch and search for notes. I can save them in the subject folder. I can revise it any time when I come back. If you haven't tried this app, you're really missing out.

Basil

Android user

This app has made me feel so much more confident in my exam prep, not only through boosting my own self confidence through the features that allow you to connect with others and feel less alone, but also through the way the app itself is centred around making you feel better. It is easy to navigate, fun to use, and helpful to anyone struggling in absolutely any way.

David K

iOS user

The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!

Sudenaz Ocak

Android user

In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.

Greenlight Bonnie

Android user

very reliable app to help and grow your ideas of Maths, English and other related topics in your works. please use this app if your struggling in areas, this app is key for that. wish I'd of done a review before. and it's also free so don't worry about that.

Rohan U

Android user

I know a lot of apps use fake accounts to boost their reviews but this app deserves it all. Originally I was getting 4 in my English exams and this time I got a grade 7. I didn’t even know about this app three days until the exam and it has helped A LOT. Please actually trust me and use it as I’m sure you too will see developments.

Xander S

iOS user

THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE THE SCHOOLGPT. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮

Elisha

iOS user

This apps acc the goat. I find revision so boring but this app makes it so easy to organize it all and then you can ask the freeeee ai to test yourself so good and you can easily upload your own stuff. highly recommend as someone taking mocks now

Paul T

iOS user

Subjects

Maths

Circles

Inscribed Angles

 

Maths

•

422

•

3 Mar 2023

•

5 pages

Circle Theorems Explained: Rules, Examples & Answer PDFs for Class 9 & 10

user profile picture

Shaz

@shaz2007

Circle Theorems: A Comprehensive Guide for Students

This guide provides a detailed explanation of circle theorems, essential for geometry studies in mathematics. It covers eight fundamental rules with examples and practice questions.

  • Covers key circle theorems explained with examples
  • Includes ... Show more

Circle Theorems Rule 1: Rule 2: A D Rute 3: Tangent meets Radius at 90° -B (Tangents that meet at a point are equal in length AB=BC The two

Sign up to see the contentIt's free!

Access to all documents

Improve your grades

Join milions of students

By signing up you accept Terms of Service and Privacy Policy

Additional Circle Theorem: Perpendicular to Chord

This page introduces an additional circle theorem rule that is crucial for solving more complex problems.

Definition: A perpendicular line from the center of a circle to a chord bisects the chord and forms right angles.

This theorem is particularly useful when dealing with problems involving chords and their relationships to the circle's center and circumference.

Highlight: Understanding this theorem can significantly simplify calculations in problems involving chord lengths and angles within circles.

Circle Theorems Rule 1: Rule 2: A D Rute 3: Tangent meets Radius at 90° -B (Tangents that meet at a point are equal in length AB=BC The two

Sign up to see the contentIt's free!

Access to all documents

Improve your grades

Join milions of students

By signing up you accept Terms of Service and Privacy Policy

Circle Theorem Questions: Practical Applications

This page presents a series of circle theorem questions and answers, demonstrating how to apply the rules in problem-solving scenarios.

  1. Question involving angles in the same segment: Given: Points A, B, C, and D on a circle Task: Find angle ACD Solution: ACD = 63° usingthe"bowtie"theoremusing the "bow tie" theorem
  2. Question on angles at the center and circumference: Given: Points A, B, C, and D on a circle with center O Tasks: Find angles x and y Solutions: x = 148° centerangletheoremcenter angle theorem, y = 106° cyclicquadrilateraltheoremcyclic quadrilateral theorem
  3. Complex question combining multiple theorems: Given: Circle with center O, tangent ABC, diameter BE Tasks: Find angles ABD and DEB Solutions: ABD = 54° tangent−radiustheoremtangent-radius theorem, DEB = 90° angleinsemicircletheoremangle in semicircle theorem

Example: In question 2, the solution demonstrates how angles at the center are twice the size of angles at the circumference, a key principle in circle theorems explained with examples.

Circle Theorems Rule 1: Rule 2: A D Rute 3: Tangent meets Radius at 90° -B (Tangents that meet at a point are equal in length AB=BC The two

Sign up to see the contentIt's free!

Access to all documents

Improve your grades

Join milions of students

By signing up you accept Terms of Service and Privacy Policy

Advanced Circle Theorem Problems

This page presents more challenging circle theorem questions, requiring the application of multiple rules and deeper analytical thinking.

  1. Problem involving isosceles triangles and tangents: Given: Circle with center O, points A, B, C, and tangent XCY Task: Find angle OCB Solution: OCB = 27° usingalternatesegmenttheoremandisoscelestrianglepropertiesusing alternate segment theorem and isosceles triangle properties
  2. Complex tangent problem: Given: Circle with center O, tangents PA and PB, angle APB = 86° Task: Find angle x Solution: x = 43° applyingmultipletheoremsincludingtangentpropertiesandisoscelestrianglesapplying multiple theorems including tangent properties and isosceles triangles

Highlight: These problems demonstrate how complex circle theorem problems and solutions often require a step-by-step approach, combining multiple theorems to reach the final answer.

Circle Theorems Rule 1: Rule 2: A D Rute 3: Tangent meets Radius at 90° -B (Tangents that meet at a point are equal in length AB=BC The two

Sign up to see the contentIt's free!

Access to all documents

Improve your grades

Join milions of students

By signing up you accept Terms of Service and Privacy Policy

Proof and Advanced Applications of Circle Theorems

This page focuses on proving circle theorems and solving highly complex problems, ideal for advanced students and GCSE circle theorems preparation.

  1. Proof question: Task: Prove that angle ROS = 2x, given RST = x Solution: Uses tangent-radius theorem, isosceles triangle properties, and angle sum theorems
  2. Advanced application question: Given: Circle with center O, tangent PT, straight line SOP, angle OPT = 32° Task: Find angle x Solution: x = 29° applyingmultipletheoremsandanglecalculationsapplying multiple theorems and angle calculations

Example: The proof question demonstrates how to construct a formal geometric proof using circle theorem rules, an essential skill for advanced mathematics.

Highlight: These problems are excellent practice for students preparing for difficult circle theorem questions and answers in exams.

Circle Theorems Rule 1: Rule 2: A D Rute 3: Tangent meets Radius at 90° -B (Tangents that meet at a point are equal in length AB=BC The two

Sign up to see the contentIt's free!

Access to all documents

Improve your grades

Join milions of students

By signing up you accept Terms of Service and Privacy Policy

Circle Theorems: Fundamental Rules and Applications

This page introduces eight essential circle theorem rules, providing a foundation for understanding geometric relationships within circles.

Definition: Circle theorems are geometric principles that describe relationships between angles, lines, and points in and around circles.

  1. Tangents meeting at a point are equal in length.
  2. A tangent meets a radius at a 90° angle.
  3. Two radii form an isosceles triangle.
  4. Opposite angles in a cyclic quadrilateral add up to 180°.
  5. The angle at the center is twice the size of the angle at the circumference.
  6. Angles in the same segment are equal.
  7. The angle at the circumference in a semicircle is 90°.
  8. Alternate segment theorem: Angles in alternate segments are equal.

Highlight: These rules are often combined in complex geometric problems, requiring students to apply multiple theorems simultaneously.

Example: Rule 2 and Rule 3 are frequently seen together in diagrams, where a tangent forms a right angle with a radius, and two radii create an isosceles triangle within the circle.

Can't find what you're looking for? Explore other subjects.

Students love us — and so will you.

4.9/5

App Store

4.8/5

Google Play

The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.

Stefan S

iOS user

This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.

Samantha Klich

Android user

Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.

Anna

iOS user

Best app on earth! no words because it’s too good

Thomas R

iOS user

Just amazing. Let's me revise 10x better, this app is a quick 10/10. I highly recommend it to anyone. I can watch and search for notes. I can save them in the subject folder. I can revise it any time when I come back. If you haven't tried this app, you're really missing out.

Basil

Android user

This app has made me feel so much more confident in my exam prep, not only through boosting my own self confidence through the features that allow you to connect with others and feel less alone, but also through the way the app itself is centred around making you feel better. It is easy to navigate, fun to use, and helpful to anyone struggling in absolutely any way.

David K

iOS user

The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!

Sudenaz Ocak

Android user

In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.

Greenlight Bonnie

Android user

very reliable app to help and grow your ideas of Maths, English and other related topics in your works. please use this app if your struggling in areas, this app is key for that. wish I'd of done a review before. and it's also free so don't worry about that.

Rohan U

Android user

I know a lot of apps use fake accounts to boost their reviews but this app deserves it all. Originally I was getting 4 in my English exams and this time I got a grade 7. I didn’t even know about this app three days until the exam and it has helped A LOT. Please actually trust me and use it as I’m sure you too will see developments.

Xander S

iOS user

THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE THE SCHOOLGPT. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮

Elisha

iOS user

This apps acc the goat. I find revision so boring but this app makes it so easy to organize it all and then you can ask the freeeee ai to test yourself so good and you can easily upload your own stuff. highly recommend as someone taking mocks now

Paul T

iOS user

The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.

Stefan S

iOS user

This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.

Samantha Klich

Android user

Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.

Anna

iOS user

Best app on earth! no words because it’s too good

Thomas R

iOS user

Just amazing. Let's me revise 10x better, this app is a quick 10/10. I highly recommend it to anyone. I can watch and search for notes. I can save them in the subject folder. I can revise it any time when I come back. If you haven't tried this app, you're really missing out.

Basil

Android user

This app has made me feel so much more confident in my exam prep, not only through boosting my own self confidence through the features that allow you to connect with others and feel less alone, but also through the way the app itself is centred around making you feel better. It is easy to navigate, fun to use, and helpful to anyone struggling in absolutely any way.

David K

iOS user

The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!

Sudenaz Ocak

Android user

In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.

Greenlight Bonnie

Android user

very reliable app to help and grow your ideas of Maths, English and other related topics in your works. please use this app if your struggling in areas, this app is key for that. wish I'd of done a review before. and it's also free so don't worry about that.

Rohan U

Android user

I know a lot of apps use fake accounts to boost their reviews but this app deserves it all. Originally I was getting 4 in my English exams and this time I got a grade 7. I didn’t even know about this app three days until the exam and it has helped A LOT. Please actually trust me and use it as I’m sure you too will see developments.

Xander S

iOS user

THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE THE SCHOOLGPT. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮

Elisha

iOS user

This apps acc the goat. I find revision so boring but this app makes it so easy to organize it all and then you can ask the freeeee ai to test yourself so good and you can easily upload your own stuff. highly recommend as someone taking mocks now

Paul T

iOS user